Cho các số thực x, y thỏa mãn x + y = 1, x3 + y3 = 2. Tính giá trị của biểu thức M = xy, N = x5 + y5.

x3 + y3 = (x + y)(x2 – xy + y2) = x2 – xy + y2 = (x + y)2 – 3xy = 1 – 3xy ⇔ 3xy = 1 – 2 = -1 ⇔ xy=−13 Suy ra: M=xy=−13 Lại có: x2 + y2 = (x + y)2 – 2xy = 1−2−13=1+23=53 N(x + y) = (x5 + y5)(x + y) = x6 + x5y + xy5 + y6 = (x2)3 + (y2)3 + xy(x4 + y4) = (x2 + y2)[(x2)2 – x2y2 + (y2)2] + xy[(x2)2 + 2x2y2 + (y2)2 - 2x2y2] =53x2+y22−3xy2−13532−2.−132=53532−3.−132−13.239=53.229−2327=299 Suy ra: N = x5 + y5 = 299.

Câu hỏi:

11/07/2024 715

Cho các số thực x, y thỏa mãn x + y = 1, x³ + y³ = 2.

Tính giá trị của biểu thức M = xy, N = x⁵ + y⁵.

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

x³ + y³ = (x + y)(x² – xy + y²) = x² – xy + y² = (x + y)² – 3xy = 1 – 3xy

⇔ 3xy = 1 – 2 = -1

⇔ $x y = - \frac{1}{3}$

Suy ra: $M = x y = - \frac{1}{3}$

Lại có: x² + y² = (x + y)² – 2xy = $1 - 2 (- \frac{1}{3}) = 1 + \frac{2}{3} = \frac{5}{3}$

N(x + y) = (x⁵ + y⁵)(x + y) = x⁶ + x⁵y + xy⁵ + y⁶

= (x²)³ + (y²)³ + xy(x⁴ + y⁴)

= (x² + y²)[(x²)² – x²y² + (y²)²] + xy[(x²)² + 2x²y² + (y²)² - 2x²y²]

$= \frac{5}{3} [{(x^{2} + y^{2})}^{2} - 3 {(x y)}^{2}] - \frac{1}{3} [{(\frac{5}{3})}^{2} - 2. {(- \frac{1}{3})}^{2}] = \frac{5}{3} [{(\frac{5}{3})}^{2} - 3. {(- \frac{1}{3})}^{2}] - \frac{1}{3} . \frac{23}{9} = \frac{5}{3} . \frac{22}{9} - \frac{23}{27} = \frac{29}{9}$

Suy ra: N = x⁵ + y⁵ = $\frac{29}{9}$ .

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chóp S.ABCD. M là một điểm trên cạnh SC.

a) Tìm giao điểm của AM và (SBD).

b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN).

Xem đáp án

Lời giải

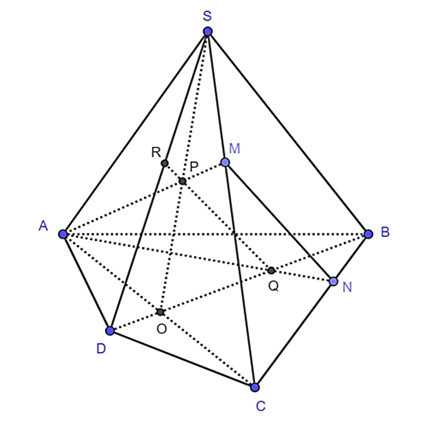
Cho hình chóp S.ABCD. M là một điểm trên cạnh SC. a) Tìm giao điểm của AM và (SBD). b) Gọi N là một điểm trên cạnh BC. Tìm giao điểm của SD và (AMN). (ảnh 1)

a) Gọi AC ∩ BD = O

Khi đó O∈(SAC) và O ∈ (SBD)

⇒ O ∈ (SAC) ∩ (SBD)

Lại có S ∈ (SAC) ∩ (SBD)

Do đó (SAC) ∩ (SBD) = SO

Gọi AM ∩ SO = P

Khi đó P ∈ AM và P ∈ SO, SO ⊂ (SBD)

Vậy AM ∩ (SBD) = P

b) Gọi AN ∩ BD = Q

Khi đó Q ∈ (AMN) và Q∈(SBD)

Lại có P ∈ (AMN) và P ∈ (SBD)

Vậy (AMN) ∩ (SBD) = PQ

Gọi PQ ∩ SD = R

Suy ra R ∈ (AMN) và R ∈ SD

Vậy SD ∩ (AMN) = R.

Câu 2

Cho tam giác nhọn ABC. Chứng minh $S_{A B C} = \frac{1}{2} . B C . B A . \sin \hat{B} = \frac{1}{2} . A B . A C . \sin \hat{A} = \frac{1}{2} . C A . C B . \sin \hat{C}$ .

Xem đáp án

Lời giải

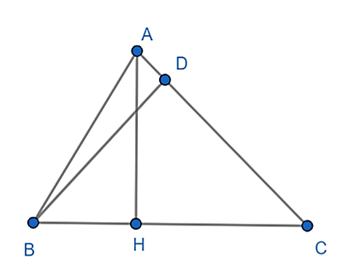
Cho tam giác nhọn ABC. Chứng minh S ABC = 1/2 BC. BA.. sin B = 1/2 AB. AC . sin A = 1/2 CA. CB. sin C (ảnh 1)

Kẻ đường cao AH, BD

$S_{A B C} = \frac{1}{2} . A H . B C$ (*)

Mà tam giác AHB vuông tại H nên: $\sin \hat{B} = \frac{A H}{A B} \Rightarrow A H = A B . \sin \hat{B}$

Khi đó: $S_{A B C} = \frac{1}{2} . A B . B C . \sin \hat{B}$

Tương tự: Trong tam giác AHC vuông tại H có: $\sin \hat{C} = \frac{A H}{A C} \Rightarrow A H = A C . \sin \hat{C}$

Khi đó: $S_{A B C} = \frac{1}{2} . A C . B C . \sin \hat{C}$

Ta có: $S_{A B C} = \frac{1}{2} . B D . A C$ (*)

Trong tam giác BAD vuông tại D có: $\sin A = \frac{B D}{A B} \Rightarrow B D = A B . \sin \hat{A}$

Thay vào (*) có:

S_{A B C} = \frac{1}{2} . B D . A C = \frac{1}{2} . A B . A C . \sin \hat{A}

Câu 3

Cho hình 20 biết a // AB, b // AB và $\hat{M A N} = 100 °$ . Tính $\hat{N_{1}}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho chóp S.ABCD. M, N lần lượt là trung điểm của SB, SD. Tìm giao điểm của (AMN) và SC.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

cho các tập hợp A = (2; +∞) và B =[m² - 7; +∞) với m > 0. Tìm m để A\B là một khoảng có độ dài bằng 16.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho Hình 21. Biết x // z, y // z và góc $\hat{C A D} = 120 °$ .

a) Tính góc $\hat{D A z}$ .

b) Tính góc $\hat{C_{1}}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hình bình hành ABCD có $\hat{B A D} = 60 °$ ; AD = 2AB. Gọi M là trung điểm của BC, N là trung điểm của AD.

a) MCND là hình thoi.

b) ABMD là hình thang cân.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử