Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Dựng đường tròn (K) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm F, E. Gọi H là giao điểm của BE và CF.
a) Chứng minh rằng AF.AB = AE.AC và AH vuông góc BC.
b) Chứng minh OA vuông góc EF.
Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O; R). Dựng đường tròn (K) đường kính BC cắt các cạnh AB, AC lần lượt tại các điểm F, E. Gọi H là giao điểm của BE và CF.
a) Chứng minh rằng AF.AB = AE.AC và AH vuông góc BC.
b) Chứng minh OA vuông góc EF.
Quảng cáo
Trả lời:
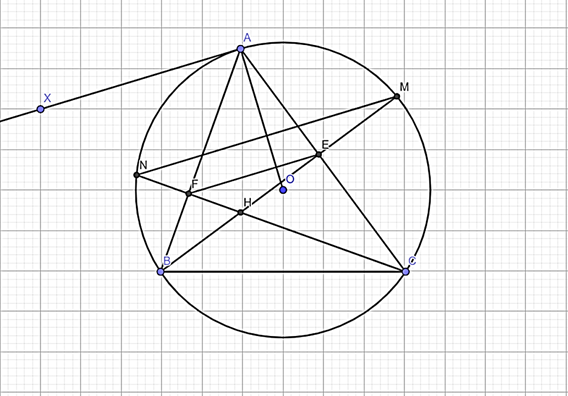
a) Ta có: (góc nội tiếp chắn nửa đường tròn (O))
Suy ra: BE, CF là hai đường cao của tam giác ABC
⇒ H là trực tâm của tam giác ABC
AH là đường cao của ABC nên AH ⊥ BC tại S
b) Vẽ tiếp tuyến Ax của (O)
Có: (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cùng chắn cung AB)
(vì cùng bù )
⇒ mà hai góc ở vị trí so le trong nên Ax // EF
Ta lại có OA ⊥ Ax (Ax là tiếp tuyến của (O)) ⇒ OA ⊥ EF.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
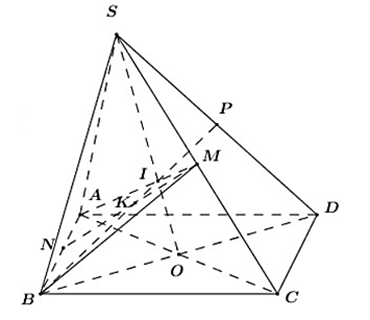
a) Trong (ABCD) gọi O = AC ∩ BD. Suy ra SO ⊂ (SAC), SO ⊂ (SBD)
Trong (SAC) gọi I = AM ∩ SO ta có:
I ∈ AM, I ∈ SO ⊂ (SBD)
Nên I ∈ (SBD)
Suy ra: I = AM ∩ (SBD)
b) Trong (SBD) gọi P = BI ∩ SD ta có:
P ∈ SD
P ∈ BI ⊂ (ABM) nên P ∈ (ABM)
Suy ra: P = SD ∩ (ABM)
Ta có: I là trọng tâm tam giác SAC nên
Xét tam giác SBD có SO là trung tuyến ứng với cạnh BD,
Nên I là trọng tâm tam giác SBD
Suy ra: BI là trung tuyến của tam giác SBD ứng với cạnh SD
Mà BI ∩ SD = P nên P là trung điểm của SD.
c) Trong (SBD) gọi K = MN ∩ BP ta có:
K ∈ MN
K ∈ BP ⊂ (SBD) nên K ∈ (SBD)
Vậy K = MN ∩ (SBD).
Lời giải
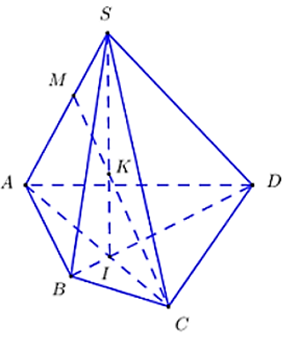
Trong (ABCD) gọi I = AC ∩ BD
Ta có: I ∈ AC ⊂ (SAC)
S ∈ (SAC)
Suy ra: SI ⊂ (SAC)
Trong (SAC) gọi K = SI ∩ MC ta có:
K ∈ MC
S ∈ SI ⊂ (SAC)
Suy ra: K = MC ∩ (SAC).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.