Ba khối 6, 7 và 8 lần lượt có 234 học sinh, 264 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối không có ai đứng lẻ hàng? Khi đó ở mỗi hàng dọc mỗi khối có bao nhiêu học sinh?
Ba khối 6, 7 và 8 lần lượt có 234 học sinh, 264 học sinh và 252 học sinh xếp thành các hàng dọc để diễu hành sao cho số hàng dọc của mỗi khối như nhau. Có thể xếp nhiều nhất thành mấy hàng dọc để mỗi khối không có ai đứng lẻ hàng? Khi đó ở mỗi hàng dọc mỗi khối có bao nhiêu học sinh?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi số hàng dọc có thể xếp nhiều nhất là x (x ∈ ℕ; x > 0}
Ta có: x ∈ ƯCLN(234; 264; 252}
234 = 2.32.13
264 = 23.3.11
252 = 22.32.7
ƯCLN(234; 264; 252) = 2.3 = 6.
Vậy có thể xếp được nhiều nhất thành 6 hàng.
Mỗi hàng của khối 6 có số học sinh là:
234 : 6 = 39 (học sinh)
Mỗi hàng của khối 7 có số học sinh là:
264 : 6 = 44 (học sinh)
Mỗi hàng của khối 88 có số học sinh là:
252 : 6 = 42 (học sinh).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
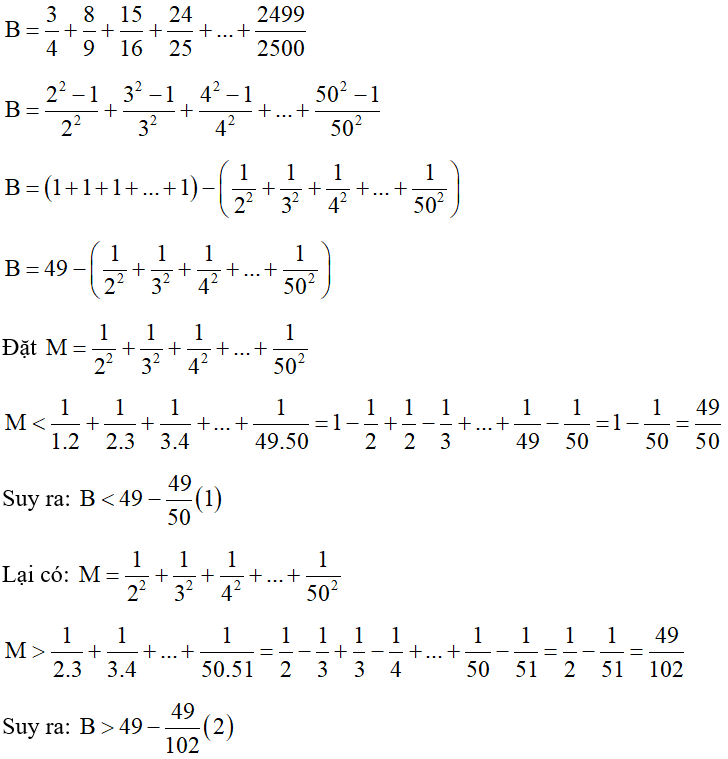
Từ (1) và (2) ta có:
⇒
Vậy B không phải là số nguyên.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo