b) Nếu giáo viên lớp chuẩn bị được tấm vải bạt dài 15m rộng 7m thì tấm vải bạt cần thêm diện tích là bao nhiêu đủ để làm hai mái và trải đáy của lều?
b) Nếu giáo viên lớp chuẩn bị được tấm vải bạt dài 15m rộng 7m thì tấm vải bạt cần thêm diện tích là bao nhiêu đủ để làm hai mái và trải đáy của lều?
Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
b) Diện tích vải bạt giáo viên chuẩn bị là:
15.7 = 105 (m2)
Vậy diện tích tấm bạt đã đủ để làm hai mái và trải đáy.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
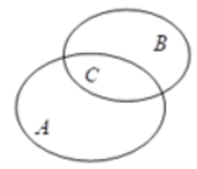
Gọi A là tập hợp các học sinh đạt học sinh giỏi môn Toán.
B là tập hợp các học sinh đạt học sinh giỏi môn Văn.
C là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
Số học sinh đạt học sinh giỏi môn Toán, Văn của lớp là: 40 – 5 = 35 (học sinh).
Theo sơ đồ Ven ta có: A + B – C = 35. ⇔ 30 + 25 – C = 35 ⇔ C = 20.
Do vậy ta có:
Số học sinh chỉ giỏi môn Toán là: A – C = 30 – 20 = 10 (học sinh).
Số học sinh chỉ giỏi môn Văn là: B – C = 25 – 20 = 5 (học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là: 10 + 5 = 15 (học sinh).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập