Câu hỏi:
18/03/2024 415Trong hộp có 100 viên bi,an và nam chơi trò chơi như sau mỗi lần chơi được bốc k viên bi ( 0 < k < 11). Người bốc bi ở lượt chơi cuối cùng là người thắng cuộc. Chứng minh rằng ai đi trước là người có chiến thuật để dành chiến thắng
Sách mới 2k7: 30 đề đánh giá năng lực DHQG Hà Nội, Tp. Hồ Chí Minh, BKHN 2025 mới nhất (600 trang - chỉ từ 140k).
Quảng cáo
Trả lời:
Ta thấy để người nào đó muốn thắng cuộc thì người đó phải làm sao bốc được viên bi cuối cùng. Suy ra đến lượt người đó lần cuối phải còn 1, 2, … hoặc 10 viên bi.
Như vậy, cứ khi nào còn lại 1, 2, … hoặc 10 viên bi và đến lượt người nào đó chơi thì người đó sẽ thắng.
Vì mỗi lượt bốc ít nhất 1 viên bi và nhiều nhất 10 viên bi, lần lượt mỗi người bốc nên người đi sau luôn có thể bốc để "kiểm soát" sao cho số bi của hai người bốc sau mỗi lượt là bằng 11. Thật vậy nếu người trước bốc 1 thì người sau bốc 10, người trước bốc 2 thì người sau bốc 9,… người trước bốc 9 thì người sau bốc 1.
Giả sử An bốc trước, An sẽ thực hiện bốc như sau:
- Lần 1 An bốc 1 viên, còn lại 99 viên.
- Lúc này đến lượt Nam bốc, Nam bốc bao nhiêu viên thì tiếp theo An bốc bù vào để được hai người bốc 11 viên trong 2 lượt liên tiếp.
Khi đó sau: 99 : 11 = 9 lần nữa thì An sẽ là người bốc cuối cùng, và An thắng cuộc.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ số 3 kim phút OP chỉ số 12. Đến khi kim phút và kim giờ gặp nhau lần đầu tiên. Tính số đo góc lượng giác mà kim giờ quét được?
Câu 2:
Trong các hàm số sau hàm số nào là hàm số chẵn:
A. y = -sinx.
B. y = cosx – sinx.
C. y = cosx + sin2x.
D. y = cosx.sinx.
Câu 3:
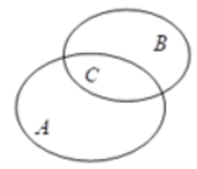
Trong 1 lớp học có 40 học sinh trong đó có 30 học sinh đạt học sinh giỏi môn toán 25 học sinh đạt học sinh giỏi môn văn biết rằng chỉ có 5 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả 2 môn toán và văn hỏi có bao nhiêu học sinh chỉ học giỏi 1 trong 2 môn toán hoặc văn.
Câu 6:
Từ hai vị trí A và B người ta quan sát một cái cây (hỉnh vẽ). Lấy C là điểm gốc cây, D là điểm ngọn của cây. A và B cùng thẳng hàng với H là điểm thuộc chiều cao CD của cây. Người ta đo được AB = 10m, HC = 2m, góc = 60°; = 45°. Tính chiều cao của cây.
về câu hỏi!