Cho 2 tập hợp M = [2m − 1; 2m + 5] và N = [m + 1; m + 7] (với m là tham số thực). Tính tổng tất cả các giá trị của m để hợp của 2 tập hợp M và N là 1 đoạn có độ dài bằng 10.

Trên đồng hồ tại thời điểm đang xét kim giờ OG chỉ số 3 kim phút OP chỉ số 12. Đến khi kim phút và kim giờ gặp nhau lần đầu tiên. Tính số đo góc lượng giác mà kim giờ quét được?

Trong các hàm số sau hàm số nào là hàm số chẵn:

A. y = -sinx.

B. y = cosx – sinx.

C. y = cosx + sin²x.

D. y = cosx.sinx.

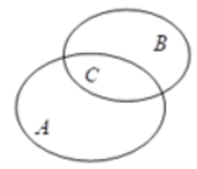
Trong 1 lớp học có 40 học sinh trong đó có 30 học sinh đạt học sinh giỏi môn toán 25 học sinh đạt học sinh giỏi môn văn biết rằng chỉ có 5 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả 2 môn toán và văn hỏi có bao nhiêu học sinh chỉ học giỏi 1 trong 2 môn toán hoặc văn.

Trong một đợt quyên góp để ủng hộ học sinh vùng khó khăn 40 học sinh lớp 11 của trường THPT X thực hiện kế hoạch quyên góp như sau: Ngày đầu tiên mỗi bạn quyên góp 2000đ, từ ngày thứ hai trở đi mỗi bạn quyên góp hơn ngày liền trước là 500đ. Hỏi sau bao nhiêu ngày thì số tiền quyên góp được là 9800000đ.

Xem hình vẽ, cho biết a// b và c ⊥ a.

a) Đường thẳng c có vuông góc với đường thẳng b không? Vì sao?

b) Cho đường thẳng d cắt hai đường thẳng a và b tại A và B. Cho biết $\widehat{A_1}=115°$. Tính số đo các góc $\widehat{B_2};\widehat{B_3};\widehat{A_3}$

c) Gọi Ax và By lần lượt là tia phân giác của các góc $\widehat{A_1};\widehat{B_3}$. Chứng minh: Ax //By.

Từ hai vị trí A và B người ta quan sát một cái cây (hỉnh vẽ). Lấy C là điểm gốc cây, D là điểm ngọn của cây. A và B cùng thẳng hàng với H là điểm thuộc chiều cao CD của cây. Người ta đo được AB = 10m, HC = 2m, góc $\widehat{A}$= 60°; $\widehat{B}$ = 45°. Tính chiều cao của cây.

Trục số là gì? Trục số dùng để làm gì?