Vẽ đồ thị các hàm số sau:

b) $y=\frac{-x-1}{x-1}$

- Tạo các thanh trượt biểu thị các tham số a, b, c, m, n

- Nhập hàm số $y=\frac{x^2+x-1}{x-1}$ vào vùng nhập lệnh.

- Nhập hai đường tiệm cận x = 1; y = x + 2.

- Ta vẽ được đồ thị hàm số như hình vẽ sau

Nhận xét

Hàm số đồng biến trên các khoảng (−∞; 0) và (2; +∞).

Hàm số nghịch biến trên các khoảng (0; 1) và (1; 2).

Đồ thị hàm số nhận x = 1 làm tiệm cận đứng và y = x + 2 làm tiệm cân xiên.

Đồ thị hàm số nhận (1; 3) làm tâm đối xứng.

Sau khi mở máy tính, ấn liên tiếp các phím SHIFT MENU và hai lần phím di chuyển xuống để mà hình hiện bảng lựa chọn.

Ấn phím 1 để chọn mục Table. Màn hình sẽ hiển thị bảng lựa chọn như hình bên dưới

Tiếp đó, ấn phím 1 để chọn dạng bảng có 1 hàm số.

Ấn các phím MENU 8 để vào chương trình Table.

Tiến hành nhập hàm số đã cho bằng cách ấn các phím sau:

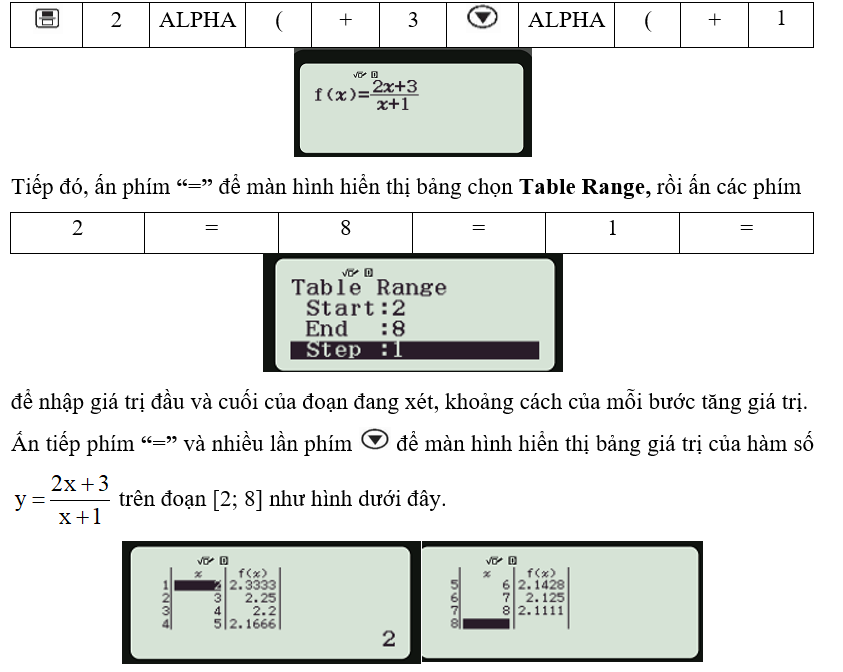
Vậy trên đoạn [2; 8], hàm số đã cho có giá trị gần đúng của giá trị lớn nhất là f(2) = 2,3333 và giá trị nhỏ nhất là f(8) = 2,1111.