Câu hỏi:

13/07/2024 700

Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 9 CTST Bài 1. Đường tròn có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

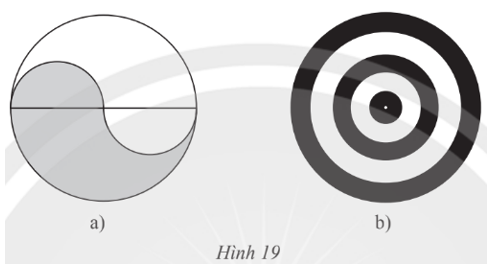
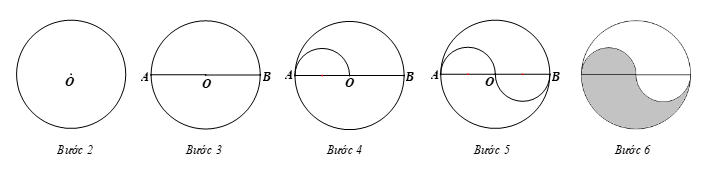
– Hình 19a):

Bước 1. Đặt đầu nhọn vào tâm đường tròn lớn, mở cung của compa sao cho đầu bút nằm trên đường tròn lớn, ta đo được bán kính của đường tròn lớn.

Bước 2. Vẽ đường tròn với bán kính ta vừa đo được, ta được đường tròn lớn.

Bước 3. Kẻ đường kính AB của đường tròn lớn.

Bước 4. Vẽ nửa đường tròn đường kính OA sao cho nửa đường tròn nằm phía trên so với AB.

Bước 5. Vẽ nửa đường tròn đường kính OB sao cho nửa đường tròn nằm phía dưới so với AB.

Bước 6. Xóa tên các điểm vừa đặt, tô màu giống Hình 19a).

Dùng compa đo bán kính và vẽ lại các hình trong Hình 19. (ảnh 2)

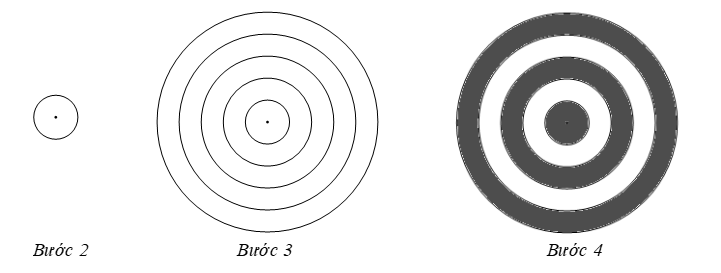
– Hình 19b):

Bước 1.

⦁ Đặt đầu nhọn vào tâm đường tròn nhỏ nhất, mở cung của compa sao cho đầu bút nằm trên đường tròn đó, ta đo được bán kính của đường tròn nhỏ nhất.

⦁ Vẽ đường tròn với bán kính ta vừa đo được, ta được đường tròn nhỏ nhất.

Bước 2.

⦁ Đặt đầu nhọn vào tâm đường tròn thứ hai, mở cung của compa sao cho đầu bút nằm trên đường tròn đó, ta đo được bán kính của đường tròn thứ hai.

⦁ Vẽ đường tròn có tâm trùng với tâm đường tròn nhỏ nhất, với bán kính ta vừa đo được, ta được đường tròn thứ hai.

Bước 3. Thực hiện lặp lại Bước 2 với 4 đường tròn còn lại.

Bước 4. Tô màu giống Hình 19b).

Dùng compa đo bán kính và vẽ lại các hình trong Hình 19. (ảnh 3)

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tứ giác ABCD có $\hat{B} = \hat{D} = 90 ° .$

a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

b) So sánh độ dài của AC và BD.

Xem đáp án

Lời giải

Cho tứ giác ABCD có góc = góc D = 90 độ a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn. (ảnh 1)

Câu 2

Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC.

a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’.

b) So sánh độ dài hai đoạn thẳng BC và B’C’.

Xem đáp án

Lời giải

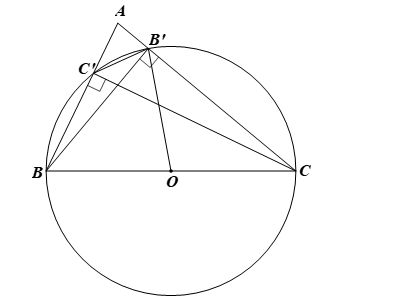
Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC. (ảnh 1)

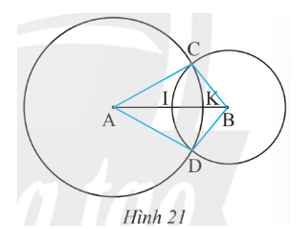
a) Xét ∆BCB’ vuông tại B’ có đường trung tuyến B’O ứng với cạnh huyền BC, do đó $B^{'} O = \frac{1}{2} B C .$

Mà O là trung điểm của BC nên $O B = O C = \frac{1}{2} B C .$

Do đó $B^{'} O = O B = O C = \frac{1}{2} B C .$

Chứng minh tương tự đối với ∆BCC’ vuông tại C’, ta cũng có $C^{'} O = O B = O C = \frac{1}{2} B C .$

Suy ra $B^{'} O = C^{'} O = O B = O C = \frac{1}{2} B C .$

Vậy đường tròn tâm O bán kính OB’ đi qua B, C, C’.

b) Xét đường tròn tâm O bán kính OB’, dây BC là đường kính đi qua tâm O, dây B’C’ là dây cung không đi qua tâm O.

Do đó BC > B’C’.

Câu 3

Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm. Gọi K, I lần lượt là giao điểm của hai đường tròn đã cho với đoạn thẳng AB (Hình 21).

a) Tính độ dài của các đoạn thẳng CA, CB, DA và DB.

b) Điểm I có phải là trung điểm của đoạn thẳng AB không?

c) Tính độ dài của đoạn thẳng IK.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 18; R = 10; R’ = 6;

b) OO’ = 2; R = 9; R’ = 3;

c) OO’ = 13; R = 8; R’ = 5;

d) OO’ = 17; R = 15; R’ = 4.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).

a) Vẽ đường tròn (C; 2 cm).
b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.

Cho tứ giác ABCD có B^=D^=90°. a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn. b) So sánh độ dài của AC và BD.

Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC. a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’. b) So sánh độ dài hai đoạn thẳng BC và B’C’.

Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm, OB = 4 cm, OC = 7 cm, OD = 5 cm. Hãy cho biết mỗi điểm A, B, C, D nằm trong, nằm trên hay nằm ngoài đường tròn (O).

Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau: a) OO’ = 18; R = 10; R’ = 6; b) OO’ = 2; R = 9; R’ = 3; c) OO’ = 13; R = 8; R’ = 5; d) OO’ = 17; R = 15; R’ = 4.

Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20). a) Vẽ đường tròn (C; 2 cm). b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tứ giác ABCD có $\hat{B} = \hat{D} = 90 ° .$

a) Chứng minh bốn điểm A, B, C, D cùng nằm trên một đường tròn.

b) So sánh độ dài của AC và BD.

Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC.

a) Chứng minh đường tròn tâm O bán kính OB’ đi qua B, C, C’.

b) So sánh độ dài hai đoạn thẳng BC và B’C’.

Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 18; R = 10; R’ = 6;

b) OO’ = 2; R = 9; R’ = 3;

c) OO’ = 13; R = 8; R’ = 5;

d) OO’ = 17; R = 15; R’ = 4.

Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20).

a) Vẽ đường tròn (C; 2 cm).
b) Đường tròn (C; 2 cm) có đi qua hai điểm O và A không? Vì sao?