Cho số phức \(z\) thỏa mãn \(\left| {z - 2} \right| = 2.\) Biết rằng tập hợp các điểm biểu diễn các số phức \(w = \left( {1 - i} \right)z + i\) là một đường tròn. Bán kính \(r\) của đường tròn đó là
Quảng cáo
Trả lời:
Cách 1: Ta có \(w = (1 - i)z + i \Leftrightarrow z = \frac{{w - i}}{{1 - i}}\)
Đặt \(w = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\)\( \Rightarrow z = \frac{{x + yi - i}}{{1 - i}}.\)
Ta có \(\left| {z - 2} \right| = 2 \Leftrightarrow \left| {\frac{{x + yi - i}}{{1 - i}} - 2} \right| = 2 \Leftrightarrow \left| {\frac{{(x + yi - i)(1 + i)}}{2} - 2} \right| = 2.\)
\( \Leftrightarrow \left| {x + xi + yi - y - i + 1 - 4} \right| = 4 \Leftrightarrow \left| {x - y - 3 + (x + y - 1)i} \right| = 4\)
\( \Leftrightarrow {\left( {x - y - 3} \right)^2} + {\left( {x + y - 1} \right)^2} = 16\)
\( \Leftrightarrow {x^2} + {y^2} + 9 - 2xy + 6y - 6x + {x^2} + {y^2} + 1 + 2xy - 2y - 2x = 16\)
\( \Leftrightarrow 2{x^2} + 2{y^2} - 8x + 4y - 6 = 0 \Leftrightarrow {x^2} + {y^2} - 4x + 2y - 3 = 0\)
Đường tròn có bán kính là \(R = \sqrt {{2^2} + {1^2} + 3} = 2\sqrt 2 .\)
Cách 2: Ta có \[w = \left( {1 - i} \right)z + i \Leftrightarrow z = \frac{{w - i}}{{1 - i}} \Leftrightarrow z - 2 = \frac{{w - i}}{{1 - i}} - 2\]
\( \Leftrightarrow z - 2 = \frac{{w - i - 2 + 2i}}{{1 - i}} = \frac{{w - 2 + i}}{{1 - i}} \Leftrightarrow \left| {z - 2} \right| = \left| {\frac{{w - 2 + i}}{{1 - i}}} \right|\).
Suy ra \(\left| {z - 2} \right| = 2 \Leftrightarrow \left| {\frac{{w - 2 + i}}{{1 - i}}} \right| = 2 \Leftrightarrow \frac{{\left| {w - 2 + i} \right|}}{{\left| {1 - i} \right|}} = 2 \Leftrightarrow \left| {w - 2 + i} \right| = 2\sqrt 2 .\) Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hàm số \(T = - 0,008{t^3} - 0,16t + 28\) với \(t \in \left[ {1\,;\,\,10} \right].\)
Ta có \(T' = - 0,024{t^2} - 0,16\) với \(t \in \left[ {1\,;\,\,10} \right].\)
Suy ra hàm số \(T\) nghịch biến trên đoạn \(\left[ {1\,;\,\,10} \right].\)
Nhiệt độ thấp nhất trong phòng đạt được là:
\({T_{\min }} = T\left( {10} \right) = - 0,008 \cdot {10^3} - 0,16 \cdot 10 + 28 = 18,4\;\,\left( {^\circ C} \right)\).
Đáp án: \(18,4\).
Câu 2
A. Chiếm tỉ lệ cao và ngày càng tăng.
B. Chiếm tỉ lệ thấp và ngày càng tăng.
C. Chiếm tỉ lệ cao và ngày càng giảm.
D. Chiếm tỉ lệ thấp và ngày càng giảm.
Lời giải
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Chính phủ liên hiệp quốc dân.
B. Ủy Ban Khởi nghĩa toàn quốc.
C. Ủy Ban lâm thời khu giải phóng.
D. Ủy Ban Dân tộc giải phóng Việt Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
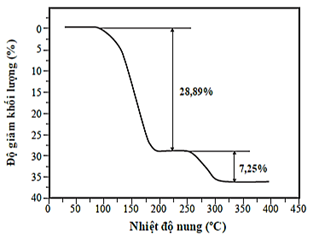
A. \({\rm{CuS}}{{\rm{O}}_4} \cdot {{\rm{H}}_2}{\rm{O}}.\)
B. \({\rm{CuS}}{{\rm{O}}_4} \cdot 4{{\rm{H}}_2}{\rm{O}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.