Câu hỏi:
19/06/2024 302
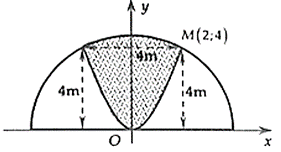
Một khuôn viên dạng nửa hình tròn có đường kính bằng m. Trên đó người ta thiết kế hai phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng bằng \[4\,\,m,\] phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí đế trồng cỏ Nhật Bản là \[100\,\,000\] đồng/m². Hỏi cần bao nhiêu tiền đế trồng cỏ Nhật Bản trên phần đất đó? (số tiền được làm tròn đến hàng nghìn).
Quảng cáo
Trả lời:
Giải bởi Vietjack
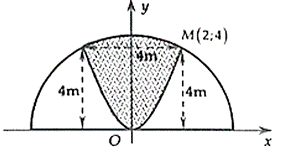
Đặt hệ trục toạ độ Oxy như hình vẽ.
Khi đó, phương trình nửa đường tròn là
\(y = \sqrt {{R^2} - {x^2}} = \sqrt {20 - {x^2}} .\)
Phương trình parabol \((P)\) có đỉnh là gốc toạ độ \(O\) nên có dạng \(y = a{x^2}.\)
Mà \((P)\) đi qua điểm \(\left( {2\,;\,\,4} \right)\) suy ra \(4 = a \cdot {2^2} \Leftrightarrow a = 1.\)
Diện tích bôi màu là \({S_1} = \int\limits_{ - 2}^2 {\left( {\sqrt {20 - {x^2}} - {x^2}} \right)\,} dx\).
Do đó, diện tích trồng cỏ là \(S = \frac{1}{2}{S_{(C)}} - {S_1} \approx 19,48\,\left( {{m^2}} \right).\)
Vậy số tiền cần tính là \[1\,\,948\,\,000\] đồng. Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \[f'\left( 1 \right) = 3 \Rightarrow a + b = 3\]. (1)
Hàm số có đạo hàm liên tục trên khoảng \[\left( {0\,;\,\, + \infty } \right)\], các điểm \(x = 1,x = \frac{1}{2}\) đều thuộc \((0; + \infty )\) nên
\(f(x) = \int {f'} (x){\rm{d}}x = \int {\left( {a{x^2} + \frac{b}{{{x^3}}}} \right)} \,\,{\rm{d}}x = \frac{{a{x^3}}}{3} - \frac{b}{{2{x^2}}} + C.\)
• \(f\left( 1 \right) = 2 \Leftrightarrow \frac{a}{3} - \frac{b}{2} + C = 2\). (2)
• \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}} \Rightarrow \frac{a}{{24}} - 2b + C = - \frac{1}{{12}}\). (3).
Từ (1), (2) và (3) ta được hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = 3}\\{\frac{a}{3} - \frac{b}{2} + C = 2}\\{\frac{a}{{24}} - 2b + C = - \frac{1}{{12}}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 1}\\{C = \frac{{11}}{6}}\end{array} \Rightarrow 2a + b = 2 \cdot 2 + 1 = 5.} \right.} \right.\)
Chọn C.
Lời giải
Gọi I là tâm của mặt cầu \((S),\,\,I \in d \Rightarrow I\left( {1 + t\,;\,\,1 + 2t\,;\,\, - 2 + t} \right).\)
\( \Rightarrow \overrightarrow {AI} = \left( {3 + t\,;\,\, - 3 + 2t\,;\,\, - 3 + t} \right)\,;\,\,\overrightarrow {BI} = \left( { - 1 + t\,;\,\,1 + 2t\,;\,\, - 5 + t} \right)\)
Vì (S) đi qua \[A,\,\,B\] nên ta có \(IA = IB \Leftrightarrow I{A^2} = I{B^2}\)
\[ \Leftrightarrow {(3 + t)^2} + {\left( { - 3 + 2t} \right)^2} + {\left( { - 3 + t} \right)^2} = {\left( { - 1 + t} \right)^2} + {\left( {1 + 2t} \right)^2} + {\left( { - 5 + t} \right)^2}\]
\( \Leftrightarrow 4t = 0 \Leftrightarrow t = 0 \Rightarrow \overrightarrow {IA} = \left( {3\,;\,\, - 3\,;\,\, - 3} \right).\)
Vậy bán kính mặt cầu \[(S)\] là \[R = IA = \sqrt {{3^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} = 3\sqrt 3 .\] Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Nhắn tin Zalo