Câu hỏi:
19/06/2024 553Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật, \(AB = a,\,\,AD = a\sqrt 3 .\) Mặt bên \[SAB\] là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng \[SD\] và mặt phẳng \(\left( {SBC} \right)\) bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
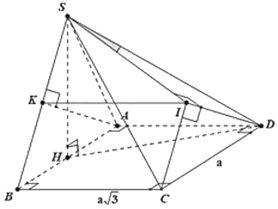
Gọi \[H\] là trung điểm của \[AB\].
Vì \(\Delta SAB\) đều nên \(SH \bot AB\).
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) do đó \(SH \bot \left( {ABCD} \right).\)
Lại có \(BC \bot AB \Rightarrow BC \bot \left( {SAB} \right)\).
Kẻ \[HF \bot SB \Rightarrow BC \bot HF \Rightarrow HF \bot \left( {SBC} \right)\].
Gọi \(DH \cap BC = E,\,\,K\) là điểm đối xứng với \(E\) qua \(F.\)
Ta có \(AD\,{\rm{//}}\,BC \Rightarrow \frac{{HD}}{{HE}} = \frac{{HA}}{{HB}} = 1 \Rightarrow HD = HE.\)
Mà \(F\) là trung điểm của \(EK\) nên \(FH\) là đường trung bình của tam giác \(EDK.\)Suy ra \(DK\,{\rm{//}}\,HF.\)Lại có \(HF \bot \left( {SBC} \right)\) nên \(DK \bot \left( {SBC} \right)\); \(\left( {SD,\,\,\left( {SBC} \right)} \right) = \left( {SD,\,\,SK} \right) = \widehat {DSK}\).
Ta có \[AH = HB = \frac{{AB}}{2} = \frac{a}{2}\]\( \Rightarrow DH = \sqrt {A{H^2} + A{D^2}} = \sqrt {\frac{{{a^2}}}{2} + 3{a^2}} = \frac{{a\sqrt {13} }}{2}.\)
Xét tam giác \(SAB\) đều cạnh \(a\) nên \(SH = \frac{{a\sqrt 3 }}{2}\)\( \Rightarrow SD = \sqrt {S{H^2} + H{D^2}} = 2a.\)
Ta có \(\frac{1}{{H{F^2}}} = \frac{1}{{H{S^2}}} + \frac{1}{{H{B^2}}} = \frac{{16}}{3} \Rightarrow HF = \frac{{a\sqrt 3 }}{4}\)\( \Rightarrow DK = 2HF = \frac{{a\sqrt 3 }}{2}\).
Lại có \(DK \bot \left( {SBC} \right) \Rightarrow DK \bot EF \Rightarrow \widehat {SKD} = 90^\circ \)\( \Rightarrow \sin \widehat {SKD} = \frac{{DK}}{{D{\rm{S}}}} = \frac{{\sqrt 3 }}{4}\)
\( \Rightarrow \cos \widehat {SKD} = \frac{{\sqrt {13} }}{4} \Rightarrow \cos \left( {SD,\,\,\left( {SBC} \right)} \right) = \frac{{\sqrt {13} }}{4}\).
Chọn A.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \[f'\left( 1 \right) = 3 \Rightarrow a + b = 3\]. (1)
Hàm số có đạo hàm liên tục trên khoảng \[\left( {0\,;\,\, + \infty } \right)\], các điểm \(x = 1,x = \frac{1}{2}\) đều thuộc \((0; + \infty )\) nên
\(f(x) = \int {f'} (x){\rm{d}}x = \int {\left( {a{x^2} + \frac{b}{{{x^3}}}} \right)} \,\,{\rm{d}}x = \frac{{a{x^3}}}{3} - \frac{b}{{2{x^2}}} + C.\)
• \(f\left( 1 \right) = 2 \Leftrightarrow \frac{a}{3} - \frac{b}{2} + C = 2\). (2)
• \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}} \Rightarrow \frac{a}{{24}} - 2b + C = - \frac{1}{{12}}\). (3).
Từ (1), (2) và (3) ta được hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = 3}\\{\frac{a}{3} - \frac{b}{2} + C = 2}\\{\frac{a}{{24}} - 2b + C = - \frac{1}{{12}}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 1}\\{C = \frac{{11}}{6}}\end{array} \Rightarrow 2a + b = 2 \cdot 2 + 1 = 5.} \right.} \right.\)
Chọn C.
Lời giải
Gọi I là tâm của mặt cầu \((S),\,\,I \in d \Rightarrow I\left( {1 + t\,;\,\,1 + 2t\,;\,\, - 2 + t} \right).\)
\( \Rightarrow \overrightarrow {AI} = \left( {3 + t\,;\,\, - 3 + 2t\,;\,\, - 3 + t} \right)\,;\,\,\overrightarrow {BI} = \left( { - 1 + t\,;\,\,1 + 2t\,;\,\, - 5 + t} \right)\)
Vì (S) đi qua \[A,\,\,B\] nên ta có \(IA = IB \Leftrightarrow I{A^2} = I{B^2}\)
\[ \Leftrightarrow {(3 + t)^2} + {\left( { - 3 + 2t} \right)^2} + {\left( { - 3 + t} \right)^2} = {\left( { - 1 + t} \right)^2} + {\left( {1 + 2t} \right)^2} + {\left( { - 5 + t} \right)^2}\]
\( \Leftrightarrow 4t = 0 \Leftrightarrow t = 0 \Rightarrow \overrightarrow {IA} = \left( {3\,;\,\, - 3\,;\,\, - 3} \right).\)
Vậy bán kính mặt cầu \[(S)\] là \[R = IA = \sqrt {{3^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} = 3\sqrt 3 .\] Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo