Câu hỏi:
19/06/2024 162
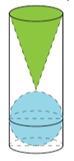
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy, một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính đáy của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Bỏ qua bề dày của lớp vỏ thủy tinh, tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy, một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính đáy của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Bỏ qua bề dày của lớp vỏ thủy tinh, tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi R là bán kính đáy của hình trụ \( \Rightarrow \) Chiều cao của hình trụ là \(h = 6R.\)
Suy ra thể tích của khối trụ ban đầu là \(V = \pi {R^2}h = 6\pi {R^3}.\)
Theo bài ra, thể tích của khối cầu trong hình là \({V_1} = \frac{4}{3}\pi {R^3}.\)
Khối nón trong hình có bán kính đáy \(r = R\); chiều cao \({h_0} = h - 2R = 4R.\)
Suy ra thể tích của khối nón là \({V_2} = \frac{1}{3}\pi r_0^2h = \frac{4}{3}\pi {R^3}.\)
Do đó, thể tích nước tràn ra ngoài cốc là \({V_0} = {V_1} + {V_2} = \frac{8}{3}\pi {R^3}.\)
Vậy tỉ số cần tìm là \(\frac{{V - {V_0}}}{V} = \frac{{6\pi {R^3} - \frac{8}{3}\pi {R^3}}}{{6\pi {R^3}}} = \frac{5}{9}.\) Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \[f'\left( 1 \right) = 3 \Rightarrow a + b = 3\]. (1)
Hàm số có đạo hàm liên tục trên khoảng \[\left( {0\,;\,\, + \infty } \right)\], các điểm \(x = 1,x = \frac{1}{2}\) đều thuộc \((0; + \infty )\) nên
\(f(x) = \int {f'} (x){\rm{d}}x = \int {\left( {a{x^2} + \frac{b}{{{x^3}}}} \right)} \,\,{\rm{d}}x = \frac{{a{x^3}}}{3} - \frac{b}{{2{x^2}}} + C.\)
• \(f\left( 1 \right) = 2 \Leftrightarrow \frac{a}{3} - \frac{b}{2} + C = 2\). (2)
• \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}} \Rightarrow \frac{a}{{24}} - 2b + C = - \frac{1}{{12}}\). (3).
Từ (1), (2) và (3) ta được hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = 3}\\{\frac{a}{3} - \frac{b}{2} + C = 2}\\{\frac{a}{{24}} - 2b + C = - \frac{1}{{12}}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 1}\\{C = \frac{{11}}{6}}\end{array} \Rightarrow 2a + b = 2 \cdot 2 + 1 = 5.} \right.} \right.\)
Chọn C.
Lời giải
Gọi I là tâm của mặt cầu \((S),\,\,I \in d \Rightarrow I\left( {1 + t\,;\,\,1 + 2t\,;\,\, - 2 + t} \right).\)
\( \Rightarrow \overrightarrow {AI} = \left( {3 + t\,;\,\, - 3 + 2t\,;\,\, - 3 + t} \right)\,;\,\,\overrightarrow {BI} = \left( { - 1 + t\,;\,\,1 + 2t\,;\,\, - 5 + t} \right)\)
Vì (S) đi qua \[A,\,\,B\] nên ta có \(IA = IB \Leftrightarrow I{A^2} = I{B^2}\)
\[ \Leftrightarrow {(3 + t)^2} + {\left( { - 3 + 2t} \right)^2} + {\left( { - 3 + t} \right)^2} = {\left( { - 1 + t} \right)^2} + {\left( {1 + 2t} \right)^2} + {\left( { - 5 + t} \right)^2}\]
\( \Leftrightarrow 4t = 0 \Leftrightarrow t = 0 \Rightarrow \overrightarrow {IA} = \left( {3\,;\,\, - 3\,;\,\, - 3} \right).\)
Vậy bán kính mặt cầu \[(S)\] là \[R = IA = \sqrt {{3^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} = 3\sqrt 3 .\] Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Nhắn tin Zalo