Câu hỏi:
21/06/2024 129
Trên tập số phức, xét phương trình \({z^2} - 2mz + {m^2} + m + 8 = 0\) (\(m\) là tham số thực). Tổng các giá trị của \(m\) để phương trình đó có hai nghiệm phân biệt \({z_1},{z_2}\) và hai điểm biểu diễn \({z_1},{z_2}\) trên mặt phẳng phức cùng với gốc tọa độ tạo thành một tam giác có diện tích bằng 3 là:
Trên tập số phức, xét phương trình \({z^2} - 2mz + {m^2} + m + 8 = 0\) (\(m\) là tham số thực). Tổng các giá trị của \(m\) để phương trình đó có hai nghiệm phân biệt \({z_1},{z_2}\) và hai điểm biểu diễn \({z_1},{z_2}\) trên mặt phẳng phức cùng với gốc tọa độ tạo thành một tam giác có diện tích bằng 3 là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \({z^2} - 2mz + {m^2} + m + 8 = 0 \Rightarrow \Delta ' = - m - 8.{\rm{ }}\)
Để phương trình có hai nghiệm phức phân biệt \( \Leftrightarrow \Delta ' < 0 \Leftrightarrow - m - 8 < 0 \Leftrightarrow m > - 8\).
Lại có \({S_{OAB}} = 3 \Leftrightarrow \frac{1}{2} \cdot OH \cdot AB = 3 \Leftrightarrow OH \cdot AB = 6.\)
\(OH = {x_{{z_1}}} = {x_{{z_2}}} = \frac{{ - b}}{{2a}} = m\); \(BA = 2BH = 2 \cdot {y_{{z_1}}} = \frac{{2 \cdot \sqrt {m + 8} }}{2} = \sqrt {m + 8} \)
\( \Rightarrow m \cdot \sqrt {m + 8} = 6\)\( \Leftrightarrow {m^2}\left( {m + 8} \right) = 36\)\( \Leftrightarrow {m^3} + 8{m^2} - 36 = 0\).
Áp dụng định lí Viète, ta có \({m_1} + {m_2} + {m_3} = \frac{{ - b}}{a} = - 8.\)
Đáp án: 8.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
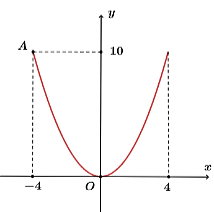
Parabol có dạng \((P):y = a{x^2}\)
\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)
Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)
Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Đáp án: 251.Lời giải
Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.
Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m < - 2}\\{m > 5}\end{array}} \right.}\\{m \ne - 11}\end{array}} \right.} \right.} \right.\).
Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận