Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 10)
114 người thi tuần này 4.6 3 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
A. \(5,55\% .\)
Lời giải
Lời giải
Giả sử trồng được \(n\) hàng cây \[\left( {n \ge 1\,,\,\,n \in \mathbb{N}} \right)\].
Số cây ở các hàng tạo thành một cấp số cộng với số hạng đầu \({u_1} = 1\) và công sai \(d = 1\).
Theo giả thiết: \[{S_n} = 3240 \Leftrightarrow \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right] = 3240\]
\( \Leftrightarrow n\left( {n + 1} \right) = 6480 \Leftrightarrow {n^2} + n - 6480 = 0\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{n = 80\,\,\,({\rm{TM}})}\\{n = - 81\,\,\,(\;{\rm{L}})}\end{array}} \right.\).
Vậy có tất cả 80 hàng cây. Chọn C.
Câu 3
Lời giải
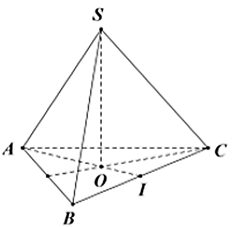
Gọi \(O\) là tâm đường tròn ngoại tiếp \(\Delta ABC\) thì \(SO \bot \left( {ABC} \right).\) Suy ra \(\widehat {SAO} = 60^\circ .\)
\(AO = \frac{2}{3} \cdot 2a \cdot \frac{{\sqrt 3 }}{2} = \frac{{2a\sqrt 3 }}{3}\,,\,\,SH = AO \cdot \tan 60^\circ = 2a.\)
Diện tích \(\Delta ABC\) là \({S_{ABC}} = \frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 .\)
Thể tích khối chóp \(S.ABC\) là \(V = \frac{1}{3} \cdot {S_{ABC}} \cdot SO = \frac{{2{a^3}\sqrt 3 }}{3}.\)
Chọn A.Câu 4
Lời giải
Ta có \(\left( {3 + 2i} \right)z + {\left( {2 - i} \right)^2} = 4 + i \Leftrightarrow \left( {3 + 2i} \right)z = 1 + 5i \Leftrightarrow z = \frac{{1 + 5i}}{{3 + 2i}} = 1 + i.\)
Suy ra \(w = \left( {z + 1} \right)\bar z = z \cdot \bar z + \bar z = \left( {1 + i} \right)\left( {1 - i} \right) + 1 - i = 2 + 1 - i = 3 - i\) \[ \Rightarrow \left| w \right| = \sqrt {10} .\]
Chọn B.
Lời giải
Do \(D \in Oy\) nên \(D\left( {0\,;\,\,y\,;\,\,0} \right)\).
Suy ra .
Khi đó \(\left[ {\overrightarrow {DA} \,,\,\,\overrightarrow {DB} } \right] = \left( {1 + 2y\,;\,\,5\,;\,\,y + 3} \right)\).
Ta có \[{V_{ABCD}} = \frac{1}{6}\left| {\left[ {\overrightarrow {DA} \,,\,\,\overrightarrow {DB} } \right] \cdot \overrightarrow {DC} } \right| = 5\]\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2y + 6 = 30}\\{2y + 6 = - 30}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{y = 12}\\{y = - 18}\end{array}} \right.} \right..\)
Vậy \({y_1} + {y_2} = 12 - 18 = - 6\). Chọn A.
Câu 6
A. \(58,1\;\,{\rm{m}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
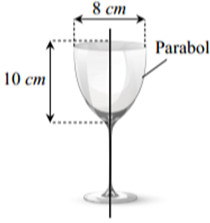
Câu 8
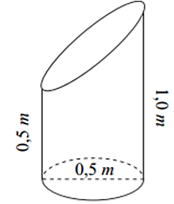
A. \(\frac{{3\pi }}{{16}}{m^3}.\)
B. \(\frac{{5\pi }}{{64}}{m^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
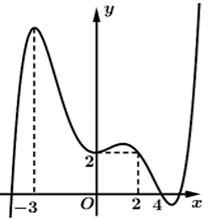
A. \(f\left( 0 \right).\)
B. \(f\left( { - 3} \right) + 6.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. chất thải.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. nhanh trí.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. cánh rừng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. lan tỏa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. tạo thành cấu trúc.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. giới thiệu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
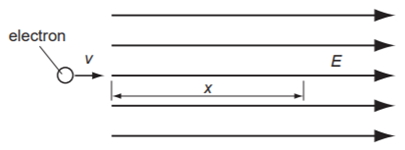
Câu 98
A. \[x = \frac{{mv}}{E}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
A. 1,4 µm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
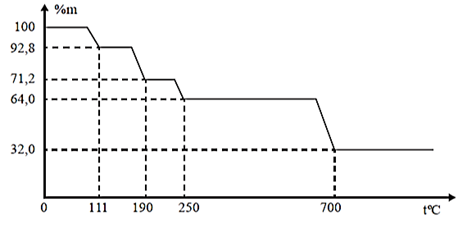
A. \({\rm{CuS}}{{\rm{O}}_{\rm{4}}}{\rm{.2}}{{\rm{H}}_{\rm{2}}}{\rm{O}}{\rm{.}}\)
B. \({\rm{CuS}}{{\rm{O}}_4} \cdot {{\rm{H}}_2}{\rm{O}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
A. Giữ khoá A và B đóng.
B. Mở cả hai khoá A và B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
…Ngày Tết, Mị cũng uống rượu. Mị lén lấy hũ rượu, cứ uống ực từng bát. Rồi say, Mị lịm mặt ngồi đấy nhìn mọi người nhảy đồng, người hát, nhưng lòng Mị thì đang sống về ngày trước. Tai Mị văng vẳng tiếng sáo gọi bạn đầu làng. Ngày trước, Mị thổi sáo giỏi. Mùa xuân này, Mị uống rượu bên bếp và thổi sáo. Mị uốn chiếc lá trên môi, thổi lá cũng hay như thổi sáo. Có biết bao nhiêu người mê, ngày đêm đã thổi sáo đi theo Mị.
Rượu đã tan lúc nào. Người về, người đi chơi đã vãn cả. Mị không biết, Mị vẫn ngồi trơ một mình giữa nhà. Mãi sau Mị mới đứng dậy, nhưng Mị không bước ra đường chơi, mà từ từ bước vào buồng. Chẳng năm nào A Sử cho Mị đi chơi Tết. Mị cũng chẳng buồn đi. Bấy giờ Mị ngồi xuống giường, trông ra cái cửa sổ lỗ vuông mờ mờ trăng trắng. Đã từ nãy, Mị thấy phơi phới trở lại, trong lòng đột nhiên vui sướng như những đêm Tết ngày trước. Mị trẻ lắm. Mị vẫn còn trẻ. Mị muốn đi chơi. Bao nhiêu người có chồng cũng đi chơi ngày Tết. Huống chi A Sử với Mị, không có lòng với nhau mà vẫn phải ở với nhau! Nếu có nắm lá ngón trong tay lúc này, Mị sẽ ăn cho chết ngay, chứ không buồn nhớ lại nữa. Nhớ lại, chỉ thấy nước mắt ứa ra. Mà tiếng sáo gọi bạn yêu vẫn lửng lơ bay ngoài đường…
(Vợ chồng A Phủ – Tô Hoài)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Một nhóm các nhà khoa học nghiên cứu về hành vi của động vật cho rằng một số loài động vật có khả năng ghi nhớ các sự việc đã diễn ra trong quá khứ, dự đoán các sự việc sắp diễn ra trong tương lai, từ đó lập kế hoạch và đưa ra lựa chọn, đồng thời có khả năng phối hợp làm việc nhóm. Tuy nhiên, những khả năng đặc biệt đó của động vật là hành động có ý thức hay hoàn toàn theo bản năng vẫn là câu hỏi chưa được giải đáp.
Trong một nghiên cứu của các nhà khoa học, có thể thấy loài ong truyền tin cho nhau biết những vị trí có thể lấy mật hoa bằng cách nhảy theo mô hình số tám. Định hướng của điệu nhảy cho biết vị trí của thức ăn so với phương hướng của mặt trời và tốc độ của điệu nhảy cho biết nguồn thức ăn cách tổ ong bao xa. Hầu hết các nhà nghiên cứu đều cho rằng khả năng biểu diễn và mã hóa điệu nhảy là bẩm sinh và không có trí thông minh đặc biệt nào tác động đến khả năng này. Nhưng trong một nghiên cứu, khi những người thử nghiệm liên tục thay đổi địa điểm của nguồn thức ăn, mỗi lần di chuyển thức ăn xa hơn 25% so với vị trí trước đó, ong mật kiếm ăn bắt đầu dự đoán nơi nguồn thức ăn sẽ xuất hiện tiếp theo. Khi các nhà nghiên cứu đến địa điểm mới, họ thấy những con ong đã đến đó trước để chờ đợi thức ăn. Vẫn chưa ai giải thích được bằng cách nào mà những con ong có bộ não chỉ nặng 113 gam lại có thể suy ra vị trí của địa điểm mới. Một nhà khoa học đã chỉ ra rằng một số loài động vật có thể sử dụng các vật dụng thô sơ trong tự nhiên để làm công cụ: rái cá dùng đá để làm nứt vỏ trai; tinh tinh mẹ hướng dẫn cho những con tinh tinh con cách sử dụng đá để mở các loại hạt cứng. Các nhà khoa học đã làm một nghiên cứu trên những con tinh tinh. Họ cho những con tinh tinh lựa chọn một trong hai căn phòng: một căn phòng để hai thùng socola, trong đó một thùng có năm hộp và một thùng có ba hộp; căn phòng còn lại họ chỉ để một thùng, nhưng trong đó có mười hộp socola, một số con tinh tinh ngay lập tức chọn căn phòng chỉ có một thùng nhưng số hộp socola nhiều hơn. Điều đó cho thấy loài tinh tinh có khả năng tính toán, so sánh và lựa chọn. Họ còn có thể đào tạo cho những con tinh tinh biết tính toán đơn giản và ghi số lượng lên nhãn dán của các mặt hàng.
(Sưu tầm)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Những người vợ nhớ chồng còn góp cho Đất Nước những núi Vọng Phu
Cặp vợ chồng yêu nhau góp nên hòn Trống Mái
Gót ngựa của Thánh Gióng đi qua còn trăm ao đầm để lại
Chín mươi chín con voi góp mình dựng đất Tổ Hùng Vương
Những con rồng nằm im góp dòng sông xanh thẳm
Người học trò nghèo góp cho Đất Nước mình núi Bút, non Nghiên.
Con cóc, con gà quê hương cùng góp cho Hạ Long thành thắng cảnh
Những người dân nào đã góp tên Ông Đốc, Ông Trang, Bà Đen, Bà Điểm
Và ở đâu trên khắp ruộng đồng gò bãi
Chẳng mang một dáng hình, một ao ước, một lối sống ông cha
Ôi Đất Nước sau bốn nghìn năm đi đâu ta cũng thấy
Những cuộc đời đã hóa núi sông ta...
(Đất nước – Nguyễn Khoa Điềm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
(1) Lơ thơ cồn nhỏ gió đìu hiu
(2) Đâu tiếng làng xa vãn chợ chiều
(3) Nắng xuống trời lên sâu chót vót
(4) Sông dài, trời rộng bến cô liêu.
(5) Bèo dạt về đâu hàng nối hàng
(6) Mênh mông không một chuyến đò ngang
(7) Không cầu gợi chút niềm thân mật
(8) Lặng lẽ bờ xanh tiếp bãi vàng.
(Tràng Giang – Huy Cận)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Tháng 6-1925, Nguyễn Ái Quốc thành lập Hội Việt Nam Cách mạng Thanh niên nhằm tổ chức và lãnh đạo quần chúng đoàn kết, tranh đấu để đánh đổ đế quốc chủ nghĩa Pháp và tay sai để tự cứu lấy mình. Cơ quan lãnh đạo cao nhất của Hội là Tổng bộ, trong đó có Nguyễn Ái Quốc, Hồ Tùng Mậu, Lê Hồng Sơn.
Báo Thanh niên của Hội do Nguyễn Ái Quốc sáng lập, ra số đầu tiên ngày 21-6 1925. Đầu năm 1927, tác phẩm Đường Kách mệnh, gồm những bài giảng của Nguyễn Ái Quốc ở các lớp huấn luyện tại Quảng Châu, được xuất bản.
Báo Thanh niên và tác phẩm Đường Kách mệnh đã trang bị lí luận cách mạng giải phóng dân tộc cho cán bộ của Hội Việt Nam Cách mạng Thanh niên để tuyên truyền đến giai cấp công nhân và các tầng lớp nhân dân Việt Nam.
Tại Quảng Châu, ngày 9-7- 1925, Nguyễn Ái Quốc đã cùng một số nhà yêu nước Triều Tiên, Inđônêxia v.v. lập ra Hội Liên hiệp các dân tộc bị áp bức ở Á Đông. Tôn chỉ của Hội là liên lạc với các dân tộc bị áp bức để cùng làm cách mạng, đánh đổ đế quốc.
Cuối năm 1928, thực hiện chủ trương "vô sản hóa", nhiều cán bộ của Hội Việt Nam Cách mạng Thanh niên đi vào các nhà máy, hầm mỏ, đồn điền, cùng sinh hoạt và lao động với công nhân để tuyên truyền vận động cách mạng, nâng cao ý thức chính trị cho giai cấp công nhân. Phong trào công nhân vì thế càng phát triển mạnh mē hơn và trở thành nòng cốt của phong trào dân tộc trong cả nước Đấu tranh của công nhân đã nổ ra ở nhiều nơi.
Các cuộc bãi công đó không chỉ bó hẹp trong phạm vi một xưởng, một địa phương, một ngành mà đã bắt đầu có sự liên kết thành phong trào chung. Cùng với bãi công của công nhân, các cuộc đấu tranh của nông dân, tiểu thương, tiểu chủ, học sinh cũng diển ra ở một số nơi".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 83-85).
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.