Đọc đoạn trích sau đây và trả lời câu hỏi:

Hắn rút dao ra, xông vào. Bá Kiến ngồi nhỏm dậy, Chí Phèo đã văng dao tới rồi. Bá Kiến chỉ kịp kêu một tiếng. Chí Phèo vừa chém túi bụi vừa kêu làng thật to. Hắn kêu làng, không bao giờ người ta vội đến. Bởi thế khi người ta đến thì hắn cũng đã đang giãy đành đạch ở giữa bao nhiêu là máu tươi. Mắt hắn trợn ngược. Mồm hắn ngáp ngáp, muốn nói, nhưng không ra tiếng. Ở cổ hắn, thỉnh thoảng máu vẫn còn ứ ra.

(Chí Phèo – Nam Cao)

Sự kịch tính của đoạn trích trên được tạo nên bởi biện pháp trần thuật nào dưới đây? 

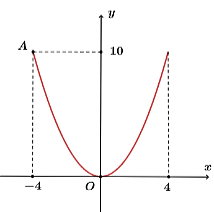
Parabol có dạng \((P):y = a{x^2}\)

\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)

Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)

Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)

Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.

Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne  - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m <  - 2}\\{m > 5}\end{array}} \right.}\\{m \ne  - 11}\end{array}} \right.} \right.} \right.\).

Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.