Câu hỏi:
08/08/2024 554
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tôi yêu chuyện cổ nước tôi
Vừa nhân hậu lại tuyệt vời sâu xa
Thương người rồi mới thương ta
Yêu nhau dù mấy cách xa cũng tìm
Ở hiền thì lại gặp hiền
Người ngay thì gặp người tiên độ trì
Mang theo chuyện cổ tôi đi
Nghe trong cuộc sống thầm thì tiếng xưa
Vàng cơn nắng, trắng cơn mưa
Con sông chảy có rặng dừa nghiêng soi.
(Chuyện cổ nước mình – Lâm Thị Mȳ Dạ)
Câu thơ “Thương người rồi mới thương ta” (in đậm) trong đoạn thơ gợi nhắc đến truyền thống nào của dân tộc Việt Nam?
A. Yêu nước. B. Nhân đạo. C. Hiếu học. D. Biết ơn nguồn cội.
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tôi yêu chuyện cổ nước tôi
Vừa nhân hậu lại tuyệt vời sâu xa
Thương người rồi mới thương ta
Yêu nhau dù mấy cách xa cũng tìm
Ở hiền thì lại gặp hiền
Người ngay thì gặp người tiên độ trì
Mang theo chuyện cổ tôi đi
Nghe trong cuộc sống thầm thì tiếng xưa
Vàng cơn nắng, trắng cơn mưa
Con sông chảy có rặng dừa nghiêng soi.
(Chuyện cổ nước mình – Lâm Thị Mȳ Dạ)
Câu thơ “Thương người rồi mới thương ta” (in đậm) trong đoạn thơ gợi nhắc đến truyền thống nào của dân tộc Việt Nam?
A. Yêu nước. B. Nhân đạo. C. Hiếu học. D. Biết ơn nguồn cội.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Câu thơ “Thương người rồi mới thương ta” gợi nhắc đến truyền thống nhân đạo (thương người) của dân tộc Việt Nam. Chọn B.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
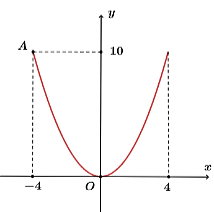
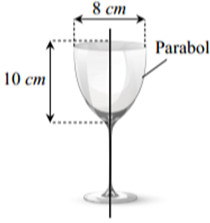
Parabol có dạng \((P):y = a{x^2}\)
\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)
Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)
Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Đáp án: 251.Lời giải
Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.
Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m < - 2}\\{m > 5}\end{array}} \right.}\\{m \ne - 11}\end{array}} \right.} \right.} \right.\).
Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận