Câu hỏi:
08/08/2024 147
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tnú hay quên chữ, nhưng đi đường núi, thì đầu nó sáng lạ lùng. Nó liên lạc cho anh Quyết từ xã lên huyện. Không bao giờ nó đi đường mòn, nó leo lên một cây cao nhìn quanh, nhìn một lượt rồi xé rừng mà đi, lọt tất cả các vòng vây. Qua sông nó không thích lội chỗ nước êm, cứ lựa chỗ thác mạnh mà bơi ngang, vượt lên trên mặt nước, cưỡi lên thác băng băng như một con cá kình. Nó nói:
– Qua chỗ nước êm thằng Mĩ – Diệm hay phục, chỗ nước mạnh nó không ngờ.
Nhưng lần đó, Tnú tới một thác sông Đắc năng, vừa cuốn cái thư của anh Quyết gửi về huyện trong một ngọn lá dong ngậm vào miệng, định vượt thác thì họng súng của giặc phục kích chĩa vào tai lạnh ngắt. Tnú chỉ kịp nuốt luôn cái thư.
(Rừng xà nu – Nguyễn Trung Thành)
Đoạn trích thể hiện tính cách nổi bật nào của nhân vật Tnú?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Tnú hay quên chữ, nhưng đi đường núi, thì đầu nó sáng lạ lùng. Nó liên lạc cho anh Quyết từ xã lên huyện. Không bao giờ nó đi đường mòn, nó leo lên một cây cao nhìn quanh, nhìn một lượt rồi xé rừng mà đi, lọt tất cả các vòng vây. Qua sông nó không thích lội chỗ nước êm, cứ lựa chỗ thác mạnh mà bơi ngang, vượt lên trên mặt nước, cưỡi lên thác băng băng như một con cá kình. Nó nói:
– Qua chỗ nước êm thằng Mĩ – Diệm hay phục, chỗ nước mạnh nó không ngờ.
Nhưng lần đó, Tnú tới một thác sông Đắc năng, vừa cuốn cái thư của anh Quyết gửi về huyện trong một ngọn lá dong ngậm vào miệng, định vượt thác thì họng súng của giặc phục kích chĩa vào tai lạnh ngắt. Tnú chỉ kịp nuốt luôn cái thư.
(Rừng xà nu – Nguyễn Trung Thành)
Đoạn trích thể hiện tính cách nổi bật nào của nhân vật Tnú?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xác định các từ khóa thể hiện tính cách của Trú: “hay quên chữ, nhưng đi đường núi, thì đầu nó sáng lạ lùng”, “xé rừng mà đi”, “lựa chỗ thác mạnh mà bơi ngang, vượt lên trên mặt nước, cưỡi lên thác băng băng”, “họng súng của giặc phục kích chĩa vào tai lạnh ngắt” → “nuốt luôn cái thư” thể hiện tính cách Tnú là người gan dạ, mưu trí và dũng cảm. Chọn B.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
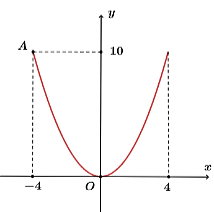
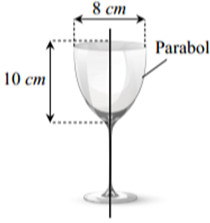
Parabol có dạng \((P):y = a{x^2}\)
\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)
Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)
Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Đáp án: 251.Lời giải
Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.
Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m < - 2}\\{m > 5}\end{array}} \right.}\\{m \ne - 11}\end{array}} \right.} \right.} \right.\).
Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận