Câu hỏi:
08/08/2024 220
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trước khi tìm hiểu kĩ hơn về việc này, đầu tiên chúng ta nên chia AI thành hai nhóm. “AI mạnh” là thuật ngữ thường được sử dụng để mô tả những cỗ máy có khả năng suy nghĩ thực sự. “AI yếu” (đôi khi còn được biết đến là “AI hẹp”) là trí thông minh được dùng để bổ sung thay vì vượt lên trí tuệ loài người. Từ trước cho tới nay, phần lớn máy móc đều được lập trình trước hoặc dạy các chuỗi hành động logic. Nhưng trong tương lai, những cỗ máy có AI mạnh sẽ có khả năng học hỏi khi chúng vận hành và phản ứng lại với các sự kiện bất ngờ. Hệ quả của việc này ư? Bạn hãy nghĩ về khả năng những việc như chẩn đoán bệnh và phẫu thuật, lập kế hoạch quân sự và ra lệnh chiến đấu, chăm sóc khách hàng được tự động hoá, những chú rô-bốt với óc sáng tạo và tính tự động nhân tạo có thể dự đoán và đối phó với tội phạm.
(Theo Ri-sát Oát-xơn, 50 ý tưởng về tương lai, Trọng Tuấn – Ngọc Thạch dịch, NXB Thế giới – Công ty cổ phần Văn hoá và Truyền thông Nhã Nam, Hà Nội, 2019, tr 120 – 125)
Nội dung chính của đoạn trích trên là gì?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Trước khi tìm hiểu kĩ hơn về việc này, đầu tiên chúng ta nên chia AI thành hai nhóm. “AI mạnh” là thuật ngữ thường được sử dụng để mô tả những cỗ máy có khả năng suy nghĩ thực sự. “AI yếu” (đôi khi còn được biết đến là “AI hẹp”) là trí thông minh được dùng để bổ sung thay vì vượt lên trí tuệ loài người. Từ trước cho tới nay, phần lớn máy móc đều được lập trình trước hoặc dạy các chuỗi hành động logic. Nhưng trong tương lai, những cỗ máy có AI mạnh sẽ có khả năng học hỏi khi chúng vận hành và phản ứng lại với các sự kiện bất ngờ. Hệ quả của việc này ư? Bạn hãy nghĩ về khả năng những việc như chẩn đoán bệnh và phẫu thuật, lập kế hoạch quân sự và ra lệnh chiến đấu, chăm sóc khách hàng được tự động hoá, những chú rô-bốt với óc sáng tạo và tính tự động nhân tạo có thể dự đoán và đối phó với tội phạm.
(Theo Ri-sát Oát-xơn, 50 ý tưởng về tương lai, Trọng Tuấn – Ngọc Thạch dịch, NXB Thế giới – Công ty cổ phần Văn hoá và Truyền thông Nhã Nam, Hà Nội, 2019, tr 120 – 125)
Nội dung chính của đoạn trích trên là gì?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nội dung chính của đoạn trích trên là: Trình bày sự phân loại của AI và dự đoán trong tương lai AI có thể thay con người làm nhiều việc.
- Đoạn trích đã trình bày 2 ý: Chia AI thành 2 nhóm (phân loại AI). Nhưng trong tương lai, những cỗ máy có AI mạnh sẽ có khả năng học hỏi khi chúng vận hành và phản ứng lại với các sự kiện bất ngờ… (dự đoán trong tương lai AI có thể thay con người làm nhiều việc). Chọn D.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
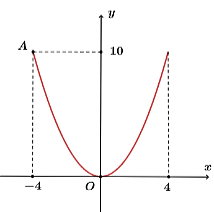
Parabol có dạng \((P):y = a{x^2}\)
\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)
Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)
Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Đáp án: 251.Lời giải
Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.
Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m < - 2}\\{m > 5}\end{array}} \right.}\\{m \ne - 11}\end{array}} \right.} \right.} \right.\).
Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo