Đọc đoạn trích sau và trả lời câu hỏi:

Ông sinh năm 1920, mất năm 2007; tên khai sinh là Nguyễn Văn Tài, quê ở làng Phù Lưu, xã Tân Hồng, huyện Từ Sơn, tỉnh Bắc Ninh. Do hoàn cảnh gia đình khó khăn, ông chỉ được học hết tiểu học, rồi vừa làm thợ sơn guốc, khắc tranh bình phong vừa viết văn. Năm 1944, ông tham gia Hội văn hóa cứu quốc, sau đó liên tục hoạt động văn nghệ phục vụ kháng chiến và cách mạng (viết văn, làm báo, diễn kịch, đóng phim).

Tác phẩm chính: Nên vợ nên chồng (tập truyện ngắn, 1955), Con chó xấu xí (tập truyện ngắn, 1962).

(Ngữ văn 12, tập hai, NXB Giáo dục Việt Nam, 2020)

Đoạn trích tiểu dẫn nói về nhà văn nào? 

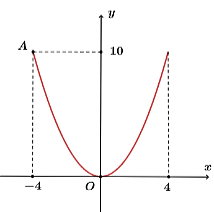
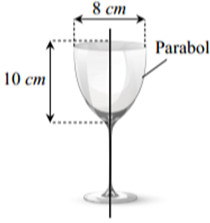
Parabol có dạng \((P):y = a{x^2}\)

\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)

Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)

Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)

Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.

Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne  - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m <  - 2}\\{m > 5}\end{array}} \right.}\\{m \ne  - 11}\end{array}} \right.} \right.} \right.\).

Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.