Câu hỏi:
08/08/2024 174
Một điểm sáng đặt tại điểm O trên trục chính của một thấu kính hội tụ (O không là quang tâm của thấu kính). Xét trục Ox vuông góc với trục chính của thấu kính với O là gốc toạ độ như hình vẽ. Tại thời điểm t = 0, điểm sáng bắt đầu dao động điều hoà dọc theo trục Ox theo phương trình \[x = A\cos \left( {2\pi t - \frac{\pi }{2}} \right){\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\], trong đó t tính bằng s. Trong khoảng thời gian \[\frac{{13}}{{12}}{\mkern 1mu} {\mkern 1mu} s\] kể từ thời điểm t = 0, điểm sáng đi được quãng đường là 18 cm. Cũng trong khoảng thời gian đó, ảnh của điểm sáng đi được quãng đường là 36 cm. Biết trong quá trình dao động, điểm sáng và ảnh của nó luôn có vận tốc ngược hướng nhau. Khoảng cách lớn nhất giữa điểm sáng và ảnh của nó trong quá trình dao động là 37 cm. Tiêu cự của thấu kính có giá trị gần nhất với giá trị nào trong các giá trị sau?
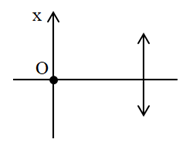
Một điểm sáng đặt tại điểm O trên trục chính của một thấu kính hội tụ (O không là quang tâm của thấu kính). Xét trục Ox vuông góc với trục chính của thấu kính với O là gốc toạ độ như hình vẽ. Tại thời điểm t = 0, điểm sáng bắt đầu dao động điều hoà dọc theo trục Ox theo phương trình \[x = A\cos \left( {2\pi t - \frac{\pi }{2}} \right){\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\], trong đó t tính bằng s. Trong khoảng thời gian \[\frac{{13}}{{12}}{\mkern 1mu} {\mkern 1mu} s\] kể từ thời điểm t = 0, điểm sáng đi được quãng đường là 18 cm. Cũng trong khoảng thời gian đó, ảnh của điểm sáng đi được quãng đường là 36 cm. Biết trong quá trình dao động, điểm sáng và ảnh của nó luôn có vận tốc ngược hướng nhau. Khoảng cách lớn nhất giữa điểm sáng và ảnh của nó trong quá trình dao động là 37 cm. Tiêu cự của thấu kính có giá trị gần nhất với giá trị nào trong các giá trị sau?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nhận xét: ảnh luôn có vận tốc ngược hướng với điểm sáng → ảnh dao động ngược pha với điểm sáng → ảnh là ảnh thật
Từ phương trình chuyển động, ta thấy pha ban đầu của điểm sáng S là \[ - \frac{\pi }{2}{\mkern 1mu} {\mkern 1mu} rad\]
→ pha ban đầu của ảnh S’ là \[\frac{\pi }{2}{\mkern 1mu} {\mkern 1mu} rad\]
Trong khoảng thời gian \[\frac{{13}}{{12}}{\mkern 1mu} {\mkern 1mu} s\], vecto quét được góc là: \[\Delta \varphi = \omega \Delta t = 2\pi .\frac{{13}}{{12}} = \frac{{13\pi }}{6} = 2\pi + \frac{\pi }{6}{\mkern 1mu} {\mkern 1mu} \left( {rad} \right)\]
Ta có vòng tròn lượng giác:
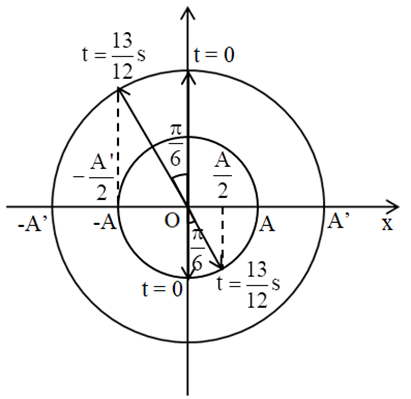
Từ vòng tròn lượng giác, ta thấy quãng đường điểm sáng S (biên độ A) và ảnh S’ (biên độ A’) đi được trong thời gian \[\frac{{13}}{{12}}{\mkern 1mu} {\mkern 1mu} s\] là: \[\left\{ {\begin{array}{*{20}{l}}{4A + \frac{A}{2} = 18{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) \Rightarrow A = 4{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\{4A' + \frac{{A'}}{2} = 36{\mkern 1mu} {\mkern 1mu} \left( {cm} \right) \Rightarrow A' = 8{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}} \right.\]\[ \Rightarrow \frac{{x'}}{x} = - \frac{{A'}}{A} = - 2 \Rightarrow x' = - 2x\]
Độ phóng đại của ảnh là: \[\left| k \right| = \left| { - \frac{{d'}}{d}} \right| = \frac{{A'}}{A} \Rightarrow \frac{{d'}}{d} = \frac{{A'}}{A} = 2 \Rightarrow d' = 2d\]
Khoảng cách giữa ảnh và vật theo phương dao động là:
\[\Delta x = \left| {x - x'} \right| = \left| {3x} \right| \Rightarrow \Delta {x_{\max }} = 3A = 12{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\]
Khoảng cách lớn nhất giữa ảnh và vật là: \[{D_{\max }} = \sqrt {{{\left( {\Delta x} \right)}^2} + {{\left( {d + d'} \right)}^2}} \Rightarrow 37 = \sqrt {{{12}^2} + {{\left( {d + d'} \right)}^2}} \]
\[ \Rightarrow d + d' = 35{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\]\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{d = \frac{{35}}{3}{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\\{d' = \frac{{70}}{3}{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)}\end{array}} \right.\]
Áp dụng công thức thấu kính, ta có: \[\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Rightarrow \frac{3}{{35}} + \frac{3}{{70}} = \frac{1}{f} \Rightarrow f = \frac{{90}}{7} \approx 7,78{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)\]
Tiêu cự của thấu kính gần nhất với giá trị 7,9 cm. Chọn C.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
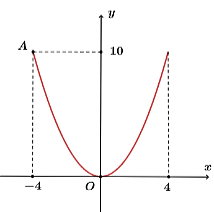
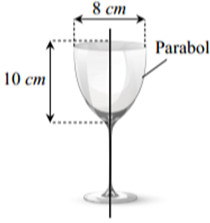
Parabol có dạng \((P):y = a{x^2}\)
\((P)\) đi qua \(A\left( { - \,4\,;\,\,10} \right)\), ta có \(10 = a{.4^2} \Leftrightarrow a = \frac{{10}}{{16}} = \frac{5}{8}\)
Suy ra parabol có phương trình \(y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y.\)
Thể tích tối đa của cốc là \(V = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)} \,{\rm{d}}y \approx 251\,\,\left( {\;{\rm{c}}{{\rm{m}}^3}} \right).\)
Đáp án: 251.Lời giải
Để đồ thị hàm số có đúng 2 đường tiệm cận đứng thì phương trình \({x^2} - 2mx + 3m + 10 = 0\) có hai nghiệm thoả mãn \({x_1},\,\,{x_2}\) phân biệt và hai nghiệm khác 1.
Nên \(\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{1 - 2m + 3m + 10 \ne 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 3m - 10 > 0}\\{m \ne - 11}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ {\begin{array}{*{20}{l}}{m < - 2}\\{m > 5}\end{array}} \right.}\\{m \ne - 11}\end{array}} \right.} \right.} \right.\).
Do \(m \in \mathbb{Z}\,,\,\,m \in \left[ { - 25\,;\,\,25} \right]\) nên có 42 giá trị nguyên \(m\) thoả mãn yêu cầu bài toán. Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận