Số nghiệm nguyên của bất phương trình \(x + 1 \ge \sqrt {2\left( {{x^2} - 1} \right)} \) là
Số nghiệm nguyên của bất phương trình \(x + 1 \ge \sqrt {2\left( {{x^2} - 1} \right)} \) là
A. 3
B. 5
C. 4
D. 2
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(x + 1 \ge \sqrt {2\left( {{x^2} - 1} \right)} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \ge 0}\\{x + 1 \ge 0}\\{{{(x + 1)}^2} \ge 2\left( {{x^2} - 1} \right)}\end{array}} \right.\)
\(\begin{array}{l}\\\left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.\\x \ge - 1\\{x^2} + 2x + 1 \ge 2\left( {{x^2} - 1} \right)\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.}\\{x \ge - 1}\\{{x^2} - 2x - 3 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\left[ \begin{array}{l}x \ge 1\\x \le - 1\end{array} \right.}\\{x \ge - 1}\\{ - 1 \le x \le 3}\end{array}} \right.\end{array}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{1 \le x \le 3}\end{array}} \right.\).
Vậy có 4 giá trị nguyên của \(x\) thỏa mãn bất phương trình. Chọn C.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(y = \frac{1}{3}{x^3} - {x^2} - mx + \frac{2}{3} \Rightarrow y' = {x^2} - 2x - m\).
Để hàm số \(y\) có đúng một điểm cực trị thuộc khoảng \(\left( {0\,;\,\,6} \right) \Leftrightarrow y' = 0\) có đúng một nghiệm thuộc khoản \(\left( {0\,;\,\,6} \right)\).
Xét hàm số \(f\left( x \right) = {x^2} - 2xf'\left( x \right) = 2x - 2\,;\,\,f'\left( x \right) = 0 \Rightarrow x = 1.\)
Ta có bảng biến thiên của \(f\left( x \right)\) như sau:
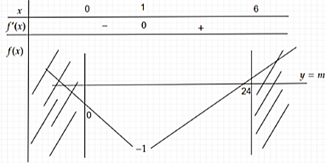
\( \Rightarrow 0 \le m < 24\)\( \Rightarrow \) Có 24 giá trị của tham số \[m.\]
Đáp án: 24.
Câu 2
A. \[56,9.\]
B. \[70,9.\]
C. \[66,3.\]
D. \[80,3.\]
Lời giải
Doanh thu của công ty tháng 7 là: \({R_7} = 6 \cdot \left( {1 + 0,1} \right)\) (tỷ đồng).
Doanh thu của công ty tháng 8 là: \({R_8} = 6 \cdot {\left( {1 + 0,1} \right)^2}\) (tỷ đồng).
......
Doanh thu của công ty tháng 12 là: \({R_{12}} = 6 \cdot {\left( {1 + 0,1} \right)^6}\) (tỷ đồng).
Tổng doanh thu từ tháng 6 là: \(TR = 6 \cdot \left( {1 + 1,1 + 1,{1^2} + 1,{1^3} + \ldots + 1,{1^6}} \right) = 56,92\) (tỷ đồng).
Suy ra, chỉ tiêu của công ty là: \(T = 56,92 - 6 + 20 = 70,92 \approx 70,9\) (tỷ đồng). Chọn B.
Câu 3
A. chính trị thiếu ổn định, dịch bệnh, nợ nước ngoài nhiều.
B. bạo lực và tệ nạn ma tuý, dân trí chưa cao, tham nhũng.
C. lạm phát, nạn tham nhũng, tỉ lệ thất nghiệp còn khá lớn.
D. quản lí yếu, gắn kết trong khu vực yếu, nạn tham nhũng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. thẳng đứng hướng từ dưới lên.
B. nằm ngang hướng từ trái sang phải.
C. thẳng đứng hướng từ trên xuống dưới.
D. nằm ngang hướng từ phải sang trái.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Mở rộng hợp tác đầu tư với các nước.
B. Phát triển nền nông nghiệp nhiệt đới.
C. Phòng chống thiên tai.
D. Phát triển kinh tế biển.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập