Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 11)
55 người thi tuần này 4.6 2.3 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
Lời giải
Câu 2
Lời giải
Phương trình vận tốc: \(v\left( t \right) = s'\left( t \right) = 3{t^2} - 4t\,\,(\;{\rm{m}}/{\rm{s}}).\)
Phương trình gia tốc: \(a\left( t \right) = v'\left( t \right) = 6t - 4\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right).\)
Tại \(t = 1,5\,\,s\) thì gia tốc tức thời của chuyển động là: \(a\left( {1,5} \right) = 6 \cdot 1,5 - 4 = 5\,\,\left( {\;{\rm{m}}/{{\rm{s}}^2}} \right).\)
Chọn C.
Lời giải
Ta có: \({\log _2}\left( {5 - {2^x}} \right) = 2 - x \Leftrightarrow 5 - {2^x} = {2^{2 - x}} \Leftrightarrow 5 \cdot {2^x} - {\left( {{2^x}} \right)^2} = 4\)
\( \Leftrightarrow {\left( {{2^x}} \right)^2} - {5.2^x} + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 4\\{2^x} = 1\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\end{array} \right.\).
Do đó \(P = {x_1} + {x_2} + {x_1}{x_2} = 2 + 0 + 2 \cdot 0 = 2.\) Chọn D.
Lời giải
Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - {{\left( {y + 1} \right)}^2} = 0}\\{\left| {x - 2} \right| - y - 1 = 0}\end{array}} \right.\).
Ta có \((2) \Leftrightarrow y + 1 = \left| {x - 2} \right| \Leftrightarrow {\left( {y + 1} \right)^2} = {\left( {x - 2} \right)^2}\).
Thay vào (1) ta được \(x - {\left( {x - 1} \right)^2} = 0 \Leftrightarrow {x^2} - 2x + 1 - x = 0\)\( \Leftrightarrow {x^2} - 3x + 1 = 0 \Leftrightarrow x = \frac{{3 \pm \sqrt 5 }}{2}{\rm{. }}\)
• Với \(x = \frac{{3 - \sqrt 5 }}{2}\) thì \(y = |x - 2| - 1 = \left| {\frac{{3 - \sqrt 5 }}{2} - 2} \right| - 1 = \frac{{1 + \sqrt 5 }}{2} - 1 = \frac{{\sqrt 5 - 1}}{2}{\rm{.}}\)
• Với\(x = \frac{{3 + \sqrt 5 }}{2}\) thì \(y = |x - 2| - 1 = \left| {\frac{{3 + \sqrt 5 }}{2} - 2} \right| - 1 = \frac{{\sqrt 5 - 1}}{2} - 1 = \frac{{\sqrt 5 - 3}}{2}{\rm{.}}\)
Vậy hệ phương trình đã cho có 2 cặp nghiệm. Chọn B.
Câu 5
A. \(w = - 6 + 4i.\)
B. \(w = 3 - 4i.\)
Lời giải
Ta có \({z_1} = - 3 + 2i\,,\,\,{z_2} = - 2 - i\,,\,\,{z_3} = 3 + i\,,\,\,{z_4} = 2 - 2i.\)
Suy ra \(w = 3{z_1} + {z_2} + {z_3} + {z_4} = 3\left( { - 3 + 2i} \right) + \left( { - 2 - i} \right) + \left( {3 + i} \right) + \left( {2 - 2i} \right)\)
\( = - 9 + 6i - 2 - i + 3 + i + 2 - 2i = \left( { - 9 - 2 + 3 + 2} \right) + \left( {6 - 1 + 1 - 2} \right)i = - 6 + 4i{\rm{. }}\)Chọn A.
Câu 6
A. \(6x + 3y + 2z - 6 = 0.\)
B. \(6x + 3y + 2z + 1 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 3
B. 5
C. 4
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
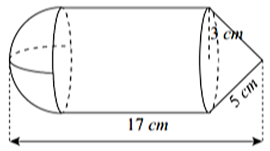
A. \(120\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
B. \(144\pi \,\,{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(V = \sqrt 3 .\)
B. \(V = 3\sqrt 3 .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
A. \((E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1.\)
B. \((E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{21}} = 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \(\left( Q \right):2x - y + 3 = 0.\)
B. \(\left( Q \right):x + z = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A. \(\left( {1\,;\,\,3} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \(6x + 9y + z + 8 = 0.\)
B. \(6x - 9y - z - 8 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
A. \(h = 2a\) và \(k = \frac{1}{8}.\)
B. \(h = 2a\) và \(k = \frac{1}{3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
A. đi sâu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
A. cho thấy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. giá trị hiện thực.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. Văn bản nghệ thuật.
B. Văn bản khoa học.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. trung tâm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
A. Văn học dân gian.
B. Văn học hiện đại.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. không những/ không những/ mà còn.
B. là/ là/ không.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
A. Chiêm nghiệm, suy tư.
B. Băn khoăn, hoài nghi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
A. Đôi bàn tay báo thù.
B. Đôi bàn tay tình nghĩa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
A. Nhân hóa, hoán dụ, so sánh, ẩn dụ.
B. Hoán dụ, so sánh, nhân hóa, nói quá.
C. So sánh, điệp cấu trúc cú pháp, nhân hóa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
A. Bóng đen sẫm như gốc cây khô cháy.
B. Mắt đăm đăm nhìn về nơi ấy.
C. Cơn mưa thăm thẳm xa khơi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
A. Tinh thần yêu nước của tác giả.
B. Nhận thức về lí tưởng cách mạng.
C. Tâm trạng của người thanh niên khi được giác ngộ lí tưởng cách mạng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
A. Cuốn hút người đọc bởi vấn đề mang tính thời sự, gây “sốc”.
B. Dẫn dắt người đọc vào vấn đề nghị luận sinh động, nóng hổi, mang tầm quốc gia.
C. Chứng minh tầm quan trọng của vấn đề nghị luận trong văn bản.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
A. Hòa nhập làm một với Đất Nước.
B. Đóng vai Đất Nước.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
A. Buồn bã, xót thương.
B. Thổn thức, ai oán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
A. Nhân vật tự bộc lộ bản thân qua lời nói, cử chỉ, hành động.
B. Người kể chuyện miêu tả nhân vật.
C. Nhân vật được đặt trong tình huống truyện.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
A. Biện pháp nghệ thuật diễn tả sự chuyển biến đột ngột trong tâm trạng của tác giả.
B. Biện pháp nghệ thuật thể hiện sự yêu đời, lãng mạn của tác giả.
C. Ước muốn táo bạo của nhà thơ để níu giữ thời gian, tuổi trẻ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
A. Cuộc đời.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
A. Biểu tượng cho sức sống và vẻ đẹp văn hóa của Hà Nội.
B. Có giá trị như một vật dụng dự báo hiệu điềm xấu, sự đổi dời.
C. Lên án sự phá hủy cảnh quan thiên nhiên của con người.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
A. Từ đơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
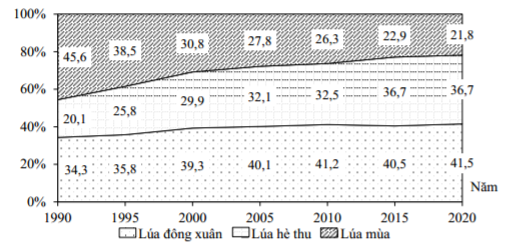
A. Năm 1990, tỉ trọng diện tích gieo trồng lúa mùa nhỏ nhất trong cơ cấu.
B. Tỉ trọng diện tích gieo trồng lúa hè thu có xu hướng giảm dần trong cả giai đoạn.
C. Tỉ trọng diện tích gieo trồng lúa mùa có xu hướng tăng dần trong cả giai đoạn.
D. Tỉ trọng diện tích gieo trồng lúa đông xuân luôn lớn nhất trong giai đoạn 2000-2020.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
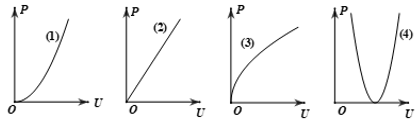
A. Đồ thị 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
A. \(45^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
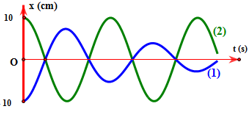
A. Hai chất điểm đều thực hiện dao động điều hòa với cùng chu kì.
B. Đồ thị (1) biểu diễn chất điểm dao động tắt dần cùng chu kì với chất điểm còn lại.
C. Hai chất điểm đều thực hiện dao động điều hòa và cùng pha ban đầu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
A. \(5\sqrt 3 \) rad/s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
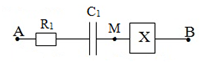
A. từ 100 MHz đến 170 MHz.
B. từ 170 MHz đến 400 MHz.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
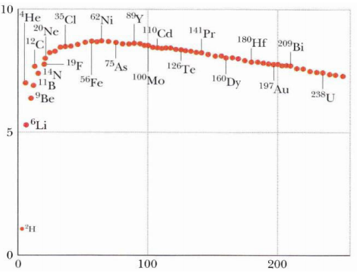
A. Hạt nhân \(^{238}U\) bền vững nhất.
B. Hạt nhân \(^{35}Cl\) bền vững hơn hạt nhân \(^{56}Fe\).
C. Hạt nhân \(^6Li\) bền vững nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
А. \[{C_3}{H_8}{O_2}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 115
A. \[{C_6}{H_{12}}{O_6}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
A. 40,12%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
A. 1 → 3 → 2.
B. 2 → 1 → 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Một quần thể ngẫu phối có thành phần kiểu gen ở thế hệ P là 0,64 AA : 0,27 Aa : 0,09 aa. Cho biết cặp gen này quy định 1 tính trạng và alen A trội hoàn toàn so với alen a. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng về quần thể này?
I. Nếu không có tác động của các nhân tố tiến hóa thì tần số các kiểu gen không thay đổi qua tất cả các thế hệ.
II. Nếu có tác động của chọn lọc tự nhiên thì tần số kiểu hình trội có thể bị thay đổi.
III. Nếu có tác động của đột biến thì tần số alen A có thể bị thay đổi.
IV. Nếu có tác động của các yếu tố ngẫu nhiên thì alen a có thể bị loại bỏ hoàn toàn khỏi quần thể.
Một quần thể ngẫu phối có thành phần kiểu gen ở thế hệ P là 0,64 AA : 0,27 Aa : 0,09 aa. Cho biết cặp gen này quy định 1 tính trạng và alen A trội hoàn toàn so với alen a. Theo lí thuyết, có bao nhiêu phát biểu sau đây đúng về quần thể này?
I. Nếu không có tác động của các nhân tố tiến hóa thì tần số các kiểu gen không thay đổi qua tất cả các thế hệ.
II. Nếu có tác động của chọn lọc tự nhiên thì tần số kiểu hình trội có thể bị thay đổi.
III. Nếu có tác động của đột biến thì tần số alen A có thể bị thay đổi.
IV. Nếu có tác động của các yếu tố ngẫu nhiên thì alen a có thể bị loại bỏ hoàn toàn khỏi quần thể.
A. 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
A. - Leu - Ala - Lys - Ala -.
B. - Leu - Lys - Ala - Ala -.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Các nhà tâm lí học về nhận thức đã có một nỗ lực to lớn hòng tìm kiếm những khác biệt về IQ giữa những người xuất thân từ nhiều vùng địa lí khác nhau nhưng hiện sống trong cùng một đất nước. Đặc biệt, nhiều nhà tâm lí học người Mĩ da trắng suốt nhiều thập kỉ qua đã ra sức chứng minh rằng người Mĩ da đen gốc Phi bẩm sinh kém thông minh hơn người Mĩ da trắng gốc Âu. Tuy nhiên, như mọi người đều biết, những người được đem ra so sánh vốn dĩ khác nhau rất nhiều về môi trường xã hội và cơ hội học hành. Sự thật này càng gây khó khăn gấp đôi cho những nỗ lực nhằm kiểm chứng giả thiết rằng những khác biệt về trí tuệ là nguyên nhân sâu xa cho những khác biệt về công nghệ. Thứ nhất, ngay cả khả năng nhận thức của người lớn đã chịu ảnh hưởng nặng nề của môi trường xã hội nơi chúng ta trải qua thời thơ ấu, khiến cho thật khó lòng phân biệt rạch ròi xem ảnh hưởng nào là do những khác biệt bẩm sinh trong gen di truyền. Thứ hai, các thử nghiệm về khả năng nhận thức (chẳng hạn như thử nghiệm IQ) có xu hướng đo đếm vốn kiến thức về văn hóa chứ không phải trí thông minh bẩm sinh dù nó là thế nào đi chăng nữa. Do những tác động rõ ràng đó của môi trường sống thời thơ ấu và tri thức thu nhận được đối với kết quả thử nghiệm IQ, nên nỗ lực của các nhà tâm lí học cho đến nay vẫn chưa thể đưa ra kết luận nào đủ sức thuyết phục về sự thiếu hụt IQ bẩm sinh mà nhiều người cho là hiển nhiên không phải bàn ở những ai không phải người da trắng.
(Jared Diamond, Súng, vi trùng và thép, NXB Thế giới, 2021, tr.24)
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Đọc sách không cốt lấy nhiều, quan trọng nhất là phải chọn cho tinh, đọc cho kĩ. Nếu đọc được mười quyển sách không quan trọng, không bằng đem thời gian, sức lực đọc mười quyển ấy mà đọc một quyển thật sự có giá trị. Nếu đọc được mười quyển sách mà chỉ lướt qua, không bằng chỉ lấy một quyển mà đọc mười lần. “Sách cũ trăm lần xem chẳng chán - Thuộc lòng, ngẫm kĩ một mình hay”, hai câu thơ đó đáng làm lời răn cho mỗi người đọc sách... Đọc ít mà đọc kĩ, thì sẽ tập thành nếp suy nghĩ sâu xa, trầm ngâm tích luỹ, tưởng tượng tự do đến mức làm đổi thay khí chất; đọc nhiều mà không chịu nghĩ sâu, như cưỡi ngựa qua chợ, tuy châu báu phơi đầy, chỉ tổ làm mắt hoa, ý loạn, tay không mà về. Thế gian có biết bao người đọc sách chỉ để trang trí bộ mặt, như kẻ trọc phú khoe của chỉ biết lấy nhiều làm quý. Đối với việc học tập, cách đó chỉ là lừa mình dối người, đối với việc làm người thì cách đó thể hiện phẩm chất tầm thường, thấp kém.
Sách đọc nên chia làm mấy loại, một loại là sách đọc để có kiến thức phổ thông mà mọi công dân thế giới hiện nay đều phải biết, một loại là sách đọc để trau dồi học vấn chuyên môn. Muốn có kiến thức phổ thông, hiện nay các bài học ở trung học và năm đầu đại học, nếu chăm chỉ học tập thì cũng đủ dùng. Nếu chăm chỉ học tập mà chỉ đọc thuộc giáo trình thì chẳng có ích lợi gì, mỗi môn phải chọn lấy từ 3 đến 5 quyển xem cho kĩ. Môn học kiến thức phổ thông tổng số không quá mười mấy môn, mỗi môn chọn từ 3 đến 5 quyển, tổng cộng số sách cần đọc cũng chẳng qua trên dưới 50 quyển. Đây không thể xem là đòi hỏi quá đáng. Nói chung số sách mà một người đã đọc, phần lớn không chỉ có thế, nếu họ không thu được lợi ích thực sự là do họ thiếu lựa chọn, khi đọc lẽ ra đọc kĩ thì họ lại đọc qua loa.
(Bàn về đọc sách – Chu Quang Tiềm)
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Không bao giờ là cuối
(Xuân Quỳnh)
Một vạt nắng cuối chiều hôm
Làm quả ngọt thêm vị mật
Hạt cây nảy thêm mầm hạt
Chút ẩm áo em vừa khô
Sau lời từ giã đi xa
Nhớ thương bắt đầu từ đấy
Tình yêu bùng như lửa cháy
Đốt lòng không chút nguôi yên
Cuối đường một bóng cây in
Đâu đã phải là chỗ hết
Nơi nghỉ để mà đi tiếp
Biết bao là chặng đường sau
Em nghĩ rất nhiều về nhau
Sau lời cuối cùng bài hát
“Hoa trắng, trời cao, gió mát
Một ngôi nhà giữa vườn xanh...”
Hết sông là biển mênh mông
Chân trời phía sau biển cả
Có khi nào đi tới đó:
Sau chân trời là vô biên
Sau sông, sau biển, sau thuyền
Sau những chân trời bát ngát
Sau bao điều cay cực nhất
Anh là hạnh phúc đời em.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Các loại vật chất tồn tại ở khắp nơi trên Trái Đất của chúng ta. Vậy, những nguyên tố cơ bản nào cấu thành vật chất?
Câu hỏi này đã được đặt ra từ hơn 2000 năm trước. Song khi đó khoa học kĩ thuật còn nhiều hạn chế nên vẫn chưa có câu trả lời chính xác. Cùng với sự phát triển của khoa học kĩ thuật, bằng nhiều thí nghiệm, nghiên cứu và phân tích khoa học, cuối cùng người ta mới đưa ra kết luận: Vạn vật trên thế giới đều được cấu thành từ một số thành phần rất đơn giản và cơ bản, như oxy, nitơ, hydro, cacbon, sắt... Các thành phần đơn giản và cơ bản này được gọi là các nguyên tố. Chúng là những vật chất đơn giản nhất nhưng không thể bị tách rời nếu sử dụng những phương pháp thông thường. Oxy và thủy ngân đều là nguyên tố, nhưng oxit thủy ngân thì lại không phải là một nguyên tố, vì chúng được cấu thành từ oxy và thủy ngân. Chúng có thể dễ dàng bị phân hủy khi nhiệt độ tăng.
Đến năm 1996, nhân loại đã phát hiện ra 112 nguyên tố khác nhau. Trong đó, 92 nguyên tố có thể tìm thấy trong tự nhiên. Những nguyên tố còn lại do các nhà khoa học chế tạo ra tại các phòng thí nghiệm. 112 nguyên tố này có màu sắc đa dạng và phong phú. Đó là kết quả của sự pha trộn khác nhau từ các màu sắc đỏ, vàng và xanh.
Bằng cách kết hợp các nguyên tố với nhau chúng có thể tạo ra rất nhiều dạng vật chất đa dạng như nguyên tố oxy kết hợp với nguyên tố hydro tạo ra nước (H2O), nguyên tố oxy kết hợp với nguyên tố cacbon tạo ra oxit cacbon (CO) và cacbonic (CO2). Hoặc bằng những cách kết hợp các hợp chất của ba nguyên tố oxy, cacbon và hydro người ta có thể tạo ra nhiều dạng vật chất mới có ứng dụng vào đời sống của con người như: Đường sacaroza (C12H22O11), rượu etylic, tinh bột (C6H10O5).... Bản thân con người chúng ta cũng được cấu thành từ hơn 20 loại nguyên tố khác nhau. Vì vậy, chúng ta có thể nói: “Không có các nguyên tố thì sẽ không có thế giới vật chất phong phú của chúng ta ngày hôm nay”.
(Sưu tầm)
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 108 đến câu 110:
"Sau đại thắng mùa Xuân 1975, Tổ quốc Việt Nam được thống nhất về lãnh thổ, song ở mỗi miền vẫn tồn tại hình thức tổ chức nhà nước khác nhau. Thực tế đó trái với nguyện vọng, tình cảm thiêng liêng của nhân dân hai miền Bắc-Nam là sớm được sum họp trong một đại gia đình, mong muốn có một chính phủ thống nhất, một cơ quan đại diện quyền lực chung cho cả nước.
Đáp lại nguyện vọng chính đáng của nhân dân cả nước, đồng thời cũng phù hợp với thực tế lịch sử dân tộc-"Nước Việt Nam là một, dân tộc Việt Nam là một-Hội nghị lần thứ 24 Ban Chấp hành Trung ương Đảng (9-1975) đề ra nhiệm vụ hoàn thành thống nhất đất nước về mặt nhà nước.
Từ ngày 15 đến ngày 21-11-1975, Hội nghị Hiệp thương chính trị thống nhất đất nước được tổ chức tại Sài Gòn. Hai đoàn đại biểu đại diện cho hai miền tham dự. Hội nghị nhất trí hoàn toàn các vấn đề về chủ trương, biện pháp nhắm thống nhất đất nước về mặt nhà nước.
Ngày 25-4-1976, cuộc Tổng tuyển cử bầu Quốc hội chung được tiến hành trong cả nước Hơn 23 triệu cử tri (chiếm 98,8% tổng số cử tri) đi bỏ phiếu và bầu ra 492 đại biểu.
Từ ngày 24-6 đến ngày 3-7-1976, Quốc hội khoá VI nước Việt Nam thống nhất kì họp đầu tiên tại Hà Nội.
Quốc hội thông qua chính sách đối nội và đối ngoại của Nhà nước Việt Nam thống nhất, quyết định tên nước là Cộng hoà xã hội chủ nghĩa Việt Nam (từ 2-7-1976), quyết định Quốc huy mang dòng chữ Cộng hoà xã hội chủ nghĩa Việt Nam, Quốc kì là lá cờ đỏ sao vàng, Quốc ca là bài Tiến quân ca, thủ đô là Hà Nội, thành phố Sài Gòn-Gia Định được đổi tên là Thành phố Hồ Chí Minh.
Quốc hội bầu các cơ quan, chức vụ lãnh đạo cao nhất của nước Cộng hoà xã hội chủ nghĩa Việt Nam, bầu Ban dự thảo Hiến pháp.
Với kết quả của kì họp thứ nhất Quốc hội khoá VI, công việc thống nhất đất nước về mặt nhà nước đã hoàn thành. Từ đây, việc tiếp tục hoàn thành thống nhất trên tất cả các lĩnh vực chính trị, tư tưởng, kinh tế, văn hoá, xã hội sẽ gắn liền với việc thực hiện những nhiệm vụ của cách mạng xã hội chủ nghĩa trong phạm vi cả nước.
Hoàn thành thống nhất đất nước về mặt nhà nước tạo nên những điều kiện chính trị cơ bản để phát huy sức mạnh toàn diện của đất nước, những điều kiện thuận lợi để cả nước đi lên chủ nghĩa xã hội, khả năng to lớn để bảo vệ Tổ quốc và mở rộng quan hệ với các nước trên thế giới".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 201-203).
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.