Để xác định hàm lượng \[C{H_3}COOH\]trong một loại acetic acid đặc bán trên thị trường, ta làm thí nghiệm sau: Cân vào cốc cân có nắp 4,00 g acid đó, hòa tan vào bình định mức 250 ml bằng nước cất. Dùng pipet lấy mỗi lần 50 ml acid đem chuẩn độ bằng dung dịch NaOH 0,5M. Kết quả trung bình sau ba lần chuẩn độ là 20 ml NaOH. Thành phần phần trăm theo khối lượng của \[C{H_3}COOH\]trong loại acetic acid đặc bán trong thị trường nói trên là:
Để xác định hàm lượng \[C{H_3}COOH\]trong một loại acetic acid đặc bán trên thị trường, ta làm thí nghiệm sau: Cân vào cốc cân có nắp 4,00 g acid đó, hòa tan vào bình định mức 250 ml bằng nước cất. Dùng pipet lấy mỗi lần 50 ml acid đem chuẩn độ bằng dung dịch NaOH 0,5M. Kết quả trung bình sau ba lần chuẩn độ là 20 ml NaOH. Thành phần phần trăm theo khối lượng của \[C{H_3}COOH\]trong loại acetic acid đặc bán trong thị trường nói trên là:
A. 40,12%.
Quảng cáo
Trả lời:
\({n_{{\rm{NaOH}}}} = 0,02 \cdot 0,5 = 0,01\;{\rm{mol}}.\)
\(\begin{array}{l}{\rm{C}}{{\rm{H}}_3}{\rm{COOH}} + {\rm{NaOH}} \to {\rm{C}}{{\rm{H}}_3}{\rm{COONa}} + {{\rm{H}}_2}{\rm{O}}\\0,01 \leftarrow \quad \,\,\,\,\,\,\,\,\,\,\,0,01\end{array}\)
\( \Rightarrow {m_{{\rm{C}}{{\rm{H}}_3}{\rm{COOH}}(50{\rm{ml}})}} = 0,01.60 = 0,6{\rm{gam}}.\)
\( \Rightarrow \% {m_{{\rm{C}}{{\rm{H}}_3}{\rm{COOH}}}} = \frac{{0,6 \cdot \frac{{250}}{{50}}}}{4} \cdot 100\% = 75\% .\)
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(y = \frac{1}{3}{x^3} - {x^2} - mx + \frac{2}{3} \Rightarrow y' = {x^2} - 2x - m\).
Để hàm số \(y\) có đúng một điểm cực trị thuộc khoảng \(\left( {0\,;\,\,6} \right) \Leftrightarrow y' = 0\) có đúng một nghiệm thuộc khoản \(\left( {0\,;\,\,6} \right)\).
Xét hàm số \(f\left( x \right) = {x^2} - 2xf'\left( x \right) = 2x - 2\,;\,\,f'\left( x \right) = 0 \Rightarrow x = 1.\)
Ta có bảng biến thiên của \(f\left( x \right)\) như sau:
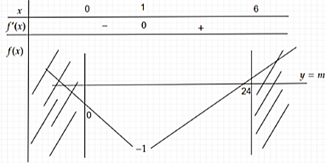
\( \Rightarrow 0 \le m < 24\)\( \Rightarrow \) Có 24 giá trị của tham số \[m.\]
Đáp án: 24.
Câu 2
Lời giải
Doanh thu của công ty tháng 7 là: \({R_7} = 6 \cdot \left( {1 + 0,1} \right)\) (tỷ đồng).
Doanh thu của công ty tháng 8 là: \({R_8} = 6 \cdot {\left( {1 + 0,1} \right)^2}\) (tỷ đồng).
......
Doanh thu của công ty tháng 12 là: \({R_{12}} = 6 \cdot {\left( {1 + 0,1} \right)^6}\) (tỷ đồng).
Tổng doanh thu từ tháng 6 là: \(TR = 6 \cdot \left( {1 + 1,1 + 1,{1^2} + 1,{1^3} + \ldots + 1,{1^6}} \right) = 56,92\) (tỷ đồng).
Suy ra, chỉ tiêu của công ty là: \(T = 56,92 - 6 + 20 = 70,92 \approx 70,9\) (tỷ đồng). Chọn B.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.