Câu hỏi:
24/06/2024 1,592Trong không gian với hệ tọa độ \[Oxyz,\] cho mặt cầu \(\left( S \right)\) có tâm \(O\), bán kính \(R = 2\) và mặt cầu \(\left( {S'} \right):{(x - 1)^2} + {y^2} + {(z - 1)^2} = 1.\) Mặt phẳng \(\left( P \right)\) thay đổi luôn tiếp xúc với hai mặt cầu \(\left( S \right)\) và \(\left( {S'} \right).\) Biết rằng \(\left( P \right)\) luôn đi qua điểm \(M(a;b;c)\) cố định. Giá trị của biểu thức \(a + b + c\) bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Mặt cầu \(\left( {S'} \right)\) có tâm \(I\left( {1\,;\,\,0\,;\,\,1} \right)\) và bán kính \(r = 1.\)
Ta có \(\overrightarrow {OI} = \left( {1\,;\,\,0\,;\,\,1} \right) \Rightarrow OI = \sqrt 2 .\)
Từ đó ta có hình vẽ mô tả vị trí tương đối của \(\left( S \right)\) và \(\left( {S'} \right)\) như sau:
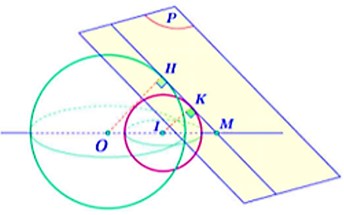
Gọi \[H,\,\,K\] lần lượt là hình chiếu vuông góc của \(O\) và \(I\) lên \((P)\) và \(M = OI \cap (P).\)
Khi đó ta có \[H,\,\,K,\,\,M\] thẳng hàng.
Xét hai tam giác đồng dạng \(\Delta OHM\) và \(\Delta IKM\) ta có: \(\frac{{MI}}{{MO}} = \frac{{IK}}{{OH}} = \frac{r}{R} = \frac{1}{2} \Rightarrow MI = \frac{1}{2}MO.\)
Suy ra \(M\) đối xứng với \(O\) qua \(I\) nên \(M\) cố định.
Mặt khác ta có \(I\) là trung điểm \[OM\] nên \(M\left( {2\,;\,\,0\,;\,\,2} \right)\).
Do đó \(a = 2\,,\,\,b = 0\,,\,\,c = 2 \Rightarrow a + b + c = 4.\) Chọn B.
Sách thầy cô Vietjack biên soạn:
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1)
Đã bán 851
₫ 150.000
₫ 39.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 290.000
₫ 140.000
Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1)
Đã bán 902
₫ 150.000
₫ 39.000
Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn)
Đã bán 1,4k
₫ 280.000
₫ 150.000
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Xem đáp án »
13/07/2024
10,187
Câu 2:
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó \[h\left( t \right)\] là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm \(t\) giây. Chiều cao của sóng (tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng) bằng
Xem đáp án »
24/06/2024
8,461
Câu 3:
Cho hàm số , với \(m\) là tham số. Gọi \({m_1},\,\,{m_2}\,\,\left( {{m_1} < {m_2}} \right)\) là các giá trị của tham số \(m\) thỏa mãn \(2{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) - {\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = 8.\) Tổng \(2{m_1} + 3{m_2}\) bằng
Xem đáp án »
24/06/2024
3,932
Câu 5:
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \,,\,\,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\) cường độ \(\overrightarrow {{F_1}} \,,\,\,\overrightarrow {{F_2}} \) lần lượt là \(300\;{\rm{N}}\) và \(400\;{\rm{N}}\,,\,\,\widehat {AMB} = 90^\circ .\) Cường độ của lực tổng hợp tác động vào vật là
Xem đáp án »
24/06/2024
3,509
Câu 6:
Polymer nào sau đây trong thành phần hóa học chỉ có hai nguyên tố C và H?
Xem đáp án »
23/07/2024
3,047
Câu 7:
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Xem đáp án »
13/07/2024
2,596
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận