Câu hỏi:
11/07/2024 203
Một loại kẹo có hình dạng là khối cầu với bán kính đáy bằng \[1{\rm{ }}cm\] được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất. Tổng diện tích tất cả các mặt xung quanh của vỏ kẹo bằng
Một loại kẹo có hình dạng là khối cầu với bán kính đáy bằng \[1{\rm{ }}cm\] được đặt trong vỏ kẹo có hình dạng là hình chóp tứ giác đều (các mặt của vỏ tiếp xúc với kẹo). Biết rằng khối chóp đều tạo thành từ vỏ kẹo đó có thể tích bé nhất. Tổng diện tích tất cả các mặt xung quanh của vỏ kẹo bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
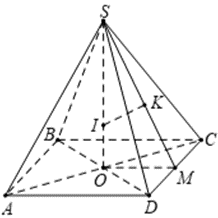
Giả sử vỏ kẹo có hình dạng là hình chóp tứ giác đều \[S.ABCD\] có đáy \[ABCD\] là hình vuông tâm \(O\), cạnh \[a,\] đường cao \(SO = h.\)
Loại kẹo có hình dạng là khối cầu có tâm \[I.\]
Gọi \(M\) là trung điểm của cạnh \[CD\]; \(K\) là hình chiếu của \(I\) trên \(SM\) nên \(K\) là hình chiếu của \(I\) trên \(\left( {SCD} \right).\) Suy ra \(OI = IK = 1.\)Dễ thấy suy ra \(\frac{{SI}}{{SM}} = \frac{{OK}}{{OM}} \Rightarrow \frac{{SO - OI}}{{\sqrt {S{O^2} + O{M^2}} }} = \frac{{IK}}{{OM}}.\)
Suy ra \(\frac{{h - 1}}{{\sqrt {{h^2} + \frac{{{a^2}}}{4}} }} = \frac{1}{{\frac{a}{2}}} \Leftrightarrow ah - a = \sqrt {4{h^2} + {a^2}} \Leftrightarrow {(ah - a)^2} = 4{h^2} + {a^2}\)
\( \Leftrightarrow {a^2}{h^2} - 2{a^2}h + {a^2} = 4{h^2} + {a^2} \Leftrightarrow \left( {{a^2} - 4} \right){h^2} - 2{a^2}h = 0 \Rightarrow h = \frac{{2{a^2}}}{{{a^2} - 4}}.\)
Thể tích khối chóp \[S.ABCD\] là: \(V = \frac{1}{3}SO \cdot {S_{ABCD}} = \frac{1}{3} \cdot \frac{{2{a^2}}}{{{a^2} - 4}} \cdot {a^2} = \frac{2}{3} \cdot \frac{{{a^4}}}{{{a^2} - 4}}\)
Lại có \(\frac{{{a^4}}}{{{a^2} - 4}} = \frac{{{a^4} - 16 + 16}}{{{a^2} - 4}} = \frac{{\left( {{a^2} - 4} \right)\left( {{a^2} + 4} \right) + 16}}{{{a^2} - 4}} = {a^2} + 4 + \frac{{16}}{{{a^2} - 4}}\)
\( = \left( {{a^2} - 4 + \frac{{16}}{{{a^2} - 4}}} \right) + 8 \ge 2\sqrt {\left( {{a^2} - 4} \right) \cdot \frac{{16}}{{{a^2} - 4}}} + 8 = 2 \cdot \sqrt {16} + 8 = 16.{\rm{ }}\)
Suy ra \(V \ge \frac{2}{3} \cdot 16 = \frac{{32}}{3}.\) Dấu xảy ra khi \(a = 2\sqrt 2 \Rightarrow h = 4 \Rightarrow OM = \sqrt 2 \,,\,\,SM = 3\sqrt 2 .\)
Vậy tổng diện tích tất cả các mặt xung quanh của vỏ kẹo là \(S = 4 \cdot {S_{SCD}} = 24\;\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Đáp án: 24.
Nhà sách vietjack
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 25 bạn chơi bóng đá, 20 bạn chơi bóng chuyền và 10 bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
Xem đáp án »
13/07/2024
9,835
Câu 2:
Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số \(h\left( t \right) = 90\cos \left( {\frac{\pi }{{10}}t} \right)\), trong đó \[h\left( t \right)\] là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm \(t\) giây. Chiều cao của sóng (tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng) bằng
Xem đáp án »
24/06/2024
8,241
Câu 3:
Cho hàm số , với \(m\) là tham số. Gọi \({m_1},\,\,{m_2}\,\,\left( {{m_1} < {m_2}} \right)\) là các giá trị của tham số \(m\) thỏa mãn \(2{\max _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) - {\min _{\left[ {0\,;\,\,2} \right]}}f\left( x \right) = 8.\) Tổng \(2{m_1} + 3{m_2}\) bằng
Xem đáp án »
24/06/2024
3,768
Câu 5:
Cho hai lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \,,\,\,\overrightarrow {{F_2}} = \overrightarrow {MB} \) cùng tác động vào một vật tại điểm \(M\) cường độ \(\overrightarrow {{F_1}} \,,\,\,\overrightarrow {{F_2}} \) lần lượt là \(300\;{\rm{N}}\) và \(400\;{\rm{N}}\,,\,\,\widehat {AMB} = 90^\circ .\) Cường độ của lực tổng hợp tác động vào vật là
Xem đáp án »
24/06/2024
3,449
Câu 6:
Polymer nào sau đây trong thành phần hóa học chỉ có hai nguyên tố C và H?
Xem đáp án »
23/07/2024
2,589
Câu 7:
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{\sqrt {x + 2} }}{{\sqrt {{x^2} - 6x + 2m} }}\) có hai đường tiệm cận đứng. Số phần tử của \(S\) là
Xem đáp án »
13/07/2024
2,485
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận