Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7. Hãy tìm các giá trị thích hợp thay vào ? ở sở đồ hình cây sau:
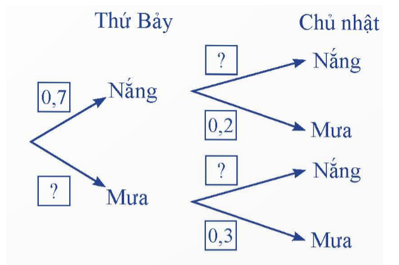
Bạn Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào thứ Bảy là 0,7. Hãy tìm các giá trị thích hợp thay vào ? ở sở đồ hình cây sau:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi A là biến cố “Ngày thứ Bảy trời nắng” và B là biến cố “Ngày Chủ nhật trời mưa”.
Khi đó P(A) = 0,7, P(B|A) = 0,2, \(P\left( {B|\overline A } \right) = 0,3\).
Suy ra \(P\left( {\overline A } \right) = 1 - P\left( A \right) = 0,3;P\left( {\overline B |A} \right) = 1 - P\left( {B|A} \right) = 0,8;\)
\(P\left( {\overline B |\overline A } \right) = 1 - P\left( {B|\overline A } \right) = 0,7\).
Áp dụng công thức nhân xác suất, ta có xác suất trời nắng vào thứ Bảy và trời mưa vào Chủ Nhật là P(AB) = P(A).P(B|A) = 0,7.0,2 = 0,14.
Tương tự ta có:
\(P\left( {A\overline B } \right) = P\left( A \right)P\left( {\overline B |A} \right) = 0,7.0,8 = 0,56\);
\(P\left( {\overline A B} \right) = P\left( {\overline A } \right)P\left( {B|\overline A } \right) = 0,3.0,3 = 0,09\);
\(P\left( {\overline A \overline B } \right) = P\left( {\overline A } \right)P\left( {\overline B |\overline A } \right) = 0,3.0,7 = 0,21\).
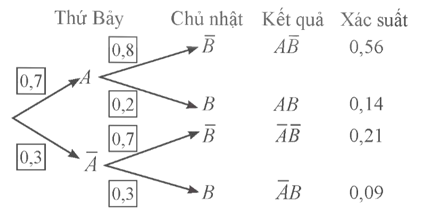
Ta có thể biểu diễn các kết quả trên theo sơ đồ hình cây như sau:
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Có \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 0,2\).
Theo công thức nhân xác suất ta có: \(P\left( {A\overline B } \right) = P\left( {\overline B } \right).P\left( {A|\overline B } \right) = 0,2.0,5 = 0,1\).
Vì \(A\overline B \) và \(AB\) là hai biến cố xung khắc và \(A\overline B \cup AB = A\).
Suy ra \(P(AB) = P(A) - P\left( {A\overline B } \right) = 0,4 - 0,1 = 0,3\).
Do đó \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P(B)}} = \frac{{0,3}}{{0,8}} = \frac{3}{8}\) .
Lời giải
Gọi M là biến cố “Viên bi lấy ra từ hộp thứ nhất có màu xanh”,
N là biến cố “Viên bi lấy ra từ hộp thứ hai có màu đỏ”.
Ta có \(P(M) = \frac{4}{{10}} = \frac{2}{5} = 0,4\); \(P(N|M) = \frac{4}{{10}} = \frac{2}{5} = 0,4\);
Suy ra \(P\left( {\overline M } \right) = 1 - P\left( M \right) = 0,6\); \(P\left( {N|\overline M } \right) = \frac{5}{{10}} = 0,5\); \(P\left( {\overline N |M} \right) = \frac{6}{{10}} = 0,6\);
\(P\left( {\overline N |\overline M } \right) = \frac{5}{{10}} = 0,5\)
Ta có sơ đồ cây
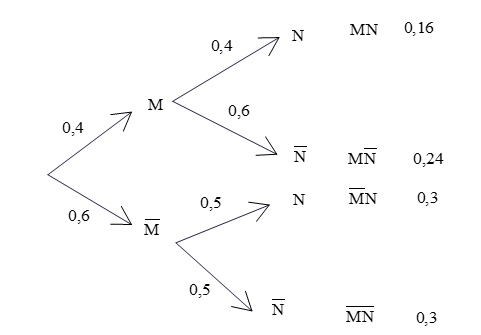
Dựa vào sơ đồ cây ta có P(A) = 0,16; P(B) = 0,24 + 0,3 = 0,54.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo