Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 17) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

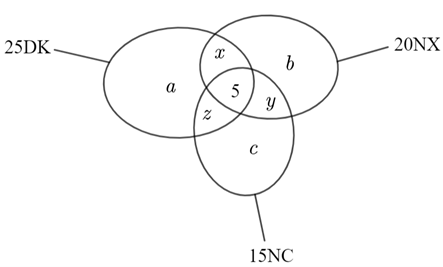
Media VietJack

Gọi \[a,\,\,b,\,\,c\] theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao;

\[x\] là số học sinh chỉ thi hai môn điền kinh và nhảy xa;

\[y\] là số học sinh chỉ thi hai môn nhảy xa và nhảy cao;

\[z\] là số học sinh chỉ thi hai môn điền kinh và nhảy cao.

Số em thi ít nhất một môn là \(45 - 7 = 38\) (học sinh).

Dựa vào biểu đồ Ven ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + x + z + 5 = 25\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)}\\{b + x + y + 5 = 20\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)}\\{c + y + z + 5 = 15\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)}\\{x + y + z + a + b + c + 5 = 38\,\,\,\,\,(4)}\end{array}} \right.\)

Cộng vế với vế của \[(1),\,\,(2),\,\,(3)\] ta được: \(a + b + c + 2\left( {x + y + z} \right) + 15 = 60\) (5)

Từ (4), (5) ta có: \(a + b + c + 2\left( {38 - 5 - a - b - c} \right) + 15 = 60 \Leftrightarrow a + b + c = 21.\)

Vậy có 21 học sinh chỉ thi một trong ba nội dung trên.

Đáp án: 21.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng

A. 3.

B. 5.

C. 10.

D. 2.

Lời giải

Ta có \(f'\left( x \right) = m \cdot \frac{1}{{2\sqrt {x - 1} }}\).

Do \(m \ne 0\) nên \(f'\left( x \right) \ne 0\) và có dấu không thay đổi \(\forall x \in \left( {1\,;\,\, + \infty } \right).\)

TH1: Nếu \(m > 0\) thì \(f'\left( x \right) > 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)

Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m.\)

Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)

\( \Leftrightarrow m + 2m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).

Do \(m > 0\) nên nhận \({m_2} = 5.\)

TH2: Nếu \(m < 0\) thì \(f'\left( x \right) < 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)

Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m.\)

Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)

\( \Leftrightarrow 2m + m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).

Do \(m < 0\) nên nhận \({m_1} = - 2.\)

Vậy \({m_1} + {m_2} = 3.\) Chọn A.

Câu 2

Đọc đoạn trích sau đây và trả lời câu hỏi:

                                             Nếu Tổ quốc neo mình đầu sóng cả

                                             Những chàng trai ra đảo đã quên mình

                                             Một sắc chỉ về Hoàng Sa thuở trước

                                             Còn truyền đời con cháu mãi đinh ninh



                                             Nếu Tổ quốc nhìn từ bao mất mát

                                             Máu xương kia dằng dặc suốt ngàn đời

                                             Hồn dân tộc ngàn năm không chịu khuất

                                             Dáng con tàu vẫn hướng mãi ra khơi.

(Nguyễn Việt Chiến, Tổ quốc nhìn từ biển, NXB Phụ nữ, 2015)

Nhân vật trữ tình đã gửi gắm cảm xúc, tâm tư gì vào đoạn thơ?

A. Những băn khoăn, trăn trở trước sự xâm lược của giặc ngoại xâm đối với biển đảo quê hương từ xưa đến nay.

B. Những suy ngẫm, tự hào về lịch sử dân tộc, trách nhiệm của mỗi con người trong công cuộc bảo vệ Tổ quốc hôm nay.

C. Sự tự hào, ngợi ca đối với vẻ đẹp và sự giàu có của biển đảo quê hương.

D. Nỗi xót xa, đau đớn trước những tấm gương anh hùng đã ngã xuống để bảo vệ biển đảo quê hương.

Lời giải

Học sinh đọc ngữ liệu, căn cứ vào các hình ảnh “chàng trai ra đảo đã quên mình, máu xương kia dằng dặc suốt ngàn đời, hồn dân tộc ngàn năm không chịu khuất” để thấy những suy ngẫm, chiêm nghiệm của tác giả, đồng thời cùng với đó là sự trân trọng, tự hào đối với lịch sử bảo vệ biển đảo, bảo vệ Tổ quốc. Học sinh căn cứ tiếp vào câu “Dáng con tàu vẫn hướng mãi ra khơi” để thấy sự tiến về phía trước của thế hệ tương lai, thể hiện trách nhiệm của thế hệ trẻ đối với công cuộc bảo vệ Tổ quốc. Chọn B.

Câu 3