Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 17)
50 người thi tuần này 4.6 2.5 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 30
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 29
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 34)
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 28
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 27
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 26
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 25
Đề thi Đánh giá năng lực ĐHQG Hà Nội phần Toán có đáp án - Đề số 24
Danh sách câu hỏi:
Câu 1
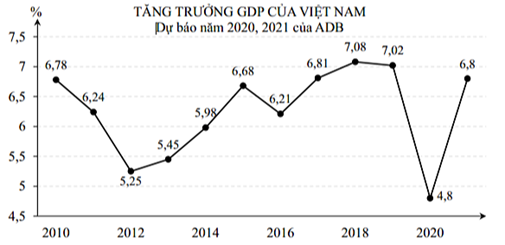
A. Từ 2010 – 2013.
B. Từ 2012 – 2015.
Lời giải
Câu 2
Lời giải
Ta có \(\overrightarrow {AB} = \left( {1\,;\,\, - 2\,;\,\, - 2} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = 3\,;\,\,\overrightarrow {BC} = \left( {4\,;\,\,1\,;\,\,1} \right) \Rightarrow \left| {\overrightarrow {BC} } \right| = 3\sqrt 2 .\)
Theo giả thiết ABCD là hình thang vuông tại \(A\) và \(B\) và có diện tích bằng \(6\sqrt 2 \) nên
\(\frac{1}{2}AB\left( {AD + BC} \right) = 6\sqrt 2 \Leftrightarrow \frac{1}{2} \cdot 3 \cdot \left( {AD + 3\sqrt 2 } \right) = 6\sqrt 2 \Rightarrow AD = \sqrt 2 \Rightarrow AD = \frac{1}{3}BC.\)
Do \[ABCD\] là hình thang vuông tại \(A\) và \(B\) nên \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {BC} .\)
Giả sử \[D\left( {a\,;\,\,b\,;\,\,c} \right)\] khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}{a - 1 = \frac{4}{3}}\\{b - 2 = \frac{1}{3}}\\{c - 1 = \frac{1}{3}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{7}{3}}\\{b = \frac{7}{3}}\\{c = \frac{4}{3}}\end{array} \Rightarrow a + b + c = 6} \right.} \right..\)
Chọn A.
Câu 3
Lời giải
Khi ô tô dừng hẳn thì \(V\left( t \right) = 0 \Leftrightarrow - 5t + 15 = 0 \Leftrightarrow t = 3\).
Quãng đường di chuyển của ô tô từ lúc hãm phanh đến khi dừng hẳn là
\(S = \int\limits_0^3 {\left( { - 5t + 15} \right)dt} = \left. {\left( { - \frac{{5{t^2}}}{2} + 15t} \right)} \right|_0^3 = 22,5\;\,({\rm{m)}}{\rm{. }}\)Chọn A.
Câu 4
A. \(50\sqrt 3 \,N.\)
Lời giải
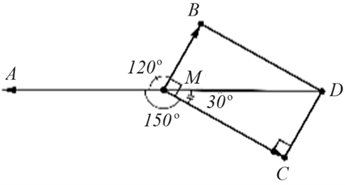
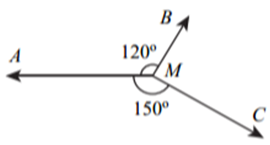
Ta có \(\widehat {AMB} = 120^\circ ,\,\,\widehat {AMC} = 150^\circ \)
\( \Rightarrow \widehat {BMC} = 360^\circ - 120^\circ - 150^\circ = 90^\circ \)
\(\widehat {CMD} = 180^\circ - \widehat {AMC} = 180^\circ - 150^\circ = 30^\circ \)
Vì vật đứng yên nên tổng hợp lực tác động vào vật bằng \(0\) nên \(MD = MA = 50\)\(\cos \widehat {CMD} = \frac{{MC}}{{MD}} \Rightarrow MC = MD \cdot \cos 30^\circ = 50 \cdot \frac{{\sqrt 3 }}{2} = 25\sqrt 3 .\)
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = {F_3} = MC = 25\sqrt 3 .\) Chọn B.
Câu 5
Lời giải
Ta có: \(\left( {3 + 2i} \right)z + {\left( {2 - i} \right)^2} = 4 + i \Leftrightarrow \left( {3 + 2i} \right)z = 1 + 5i \Leftrightarrow z = 1 + i.\)
Do đó: \[w = \left( {z + 1} \right)\bar z = z \cdot \bar z + \bar z = \left( {1 + i} \right)\left( {1 - i} \right) + 1 - i = 2 + 1 - i = 3 - i.\]
Do đó \(\left| w \right| = \sqrt {{3^2} + 1} = \sqrt {10} .\) Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. 140 triệu đồng và 180 triệu đồng.
B. 180 triệu đồng và 140 triệu đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 8.\)
B. \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 20.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \(x - y + 2z - 7 = 0.\)
B. \(2x - 2y + z - 7 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 30
A. \(\frac{{160}}{3}\,\,{\rm{c}}{{\rm{m}}^2}.\)
B. \(\frac{{140}}{3}\;\,{\rm{c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
C. \(\frac{{ - 1 + \sqrt 5 }}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 35
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
A. oan khổ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
A. trào lưu.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
A. trang bị.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 61
A. anh hùng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
A. khiến/ mà.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
A. ngẫm ngợi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
A. thiên cổ kì bút.
B. thiên cổ hùng văn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 91
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
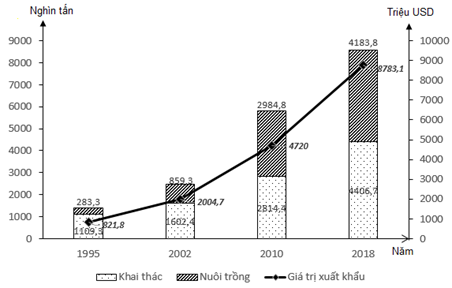
A. Sản lượng thủy sản khai thác tăng 3772,7 nghìn tấn
B. Sản lượng thủy sản nuôi trồng tăng nhanh hơn khai thác
C. Sản lượng thủy sản nuôi trồng tăng nhiều hơn khai thác
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
A. 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
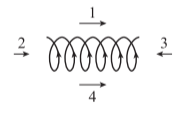
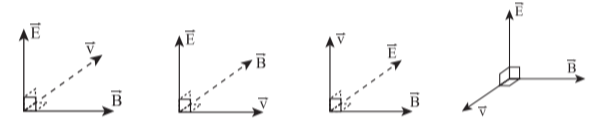
Câu 105
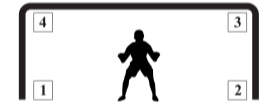
A. Hình 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 107
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 110
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 111
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
A. 50, 60, 80.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 117
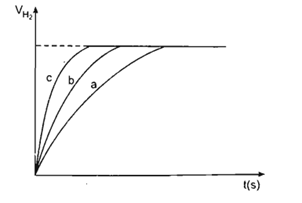
A. Khí hydrogen được giải phóng ở thí nghiệm a nhanh hơn ở thí nghiệm c.
B. Tiến hành thí nghiệm c và thí nghiệm b ở cùng 1 nhiệt độ, thì zinc ở thí nghiệm c có dạng bột, còn zinc ở thí nghiệm b có dạng lá.
C. Tiến hành thí nghiệm với zinc ở thí nghiệm a và b cùng ở dạng lá, thì nhiệt độ tiến hành thí nghiệm ở nghiệm a lớn hơn nhiệt độ tiến hành thí nghiệm ở thí nghiệm b.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 120
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 125
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 127
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Dữ dội và dịu êm
Ồn ào và lặng lẽ
Sông không hiểu nổi mình
Sóng tìm ra tận bể
Ôi con sóng ngày xưa
Và ngày sau vẫn thế
Nỗi khát vọng tình yêu
Bồi hồi trong ngực trẻ.
(Sóng – Xuân Quỳnh)
Câu 130
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Có lẽ bạn đã từng nghe về những loại thức ăn khô thiếu hấp dẫn mà các nhà du hành vũ trụ ăn trong không gian như kem khô, súp đậu sấy khô dạng bột hay thức ăn dạng viên nén. Điều đó có nghĩa là nước bị loại bỏ khỏi những thức ăn đó. Nhưng bạn có biết rằng, trong thực đơn không gian của NASA (Cơ quan Hàng không và Vũ trụ Hoa Kì) có hơn 90 loại thức ăn và nước uống khác nhau?
Nhiều loại thức ăn bị loại bỏ nước để ngăn ngừa vi khuẩn phát triển, nên cần phải thêm nước vào trước khi ăn. Một số loại thức ăn khác giống như những đồ ăn sẵn mà chúng ta hay nhìn thấy trong siêu thị, được làm nóng bằng lò vi sóng. Trên thực tế, gần đây các đầu bếp đã cung cấp thêm những bữa ăn tuyệt vời cho phi hành đoàn trong không gian. Các phi hành gia được lựa chọn các loại thức ăn yêu thích của mình ở Trái Đất và ăn thử chúng trước đó.
Bên cạnh đó, vấn đề nước uống cũng có nhiều hạn chế. Mặc dù, trong mỗi chuyến bay ra ngoài không gian, các phi hành gia mang theo rất nhiều nước nhưng đôi khi vẫn không đủ. Khi đó, họ phải sử dụng nước uống được tái chế từ nước thải của con người. Vâng, nước mà họ uống có thể là nước tiểu của một người nào đó từ vài ngày trước. Bạn sẽ không thể quá câu nệ khi bạn là một phi hành gia!
(Sưu tầm)
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 136
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
(1) Pháp chạy, Nhật hàng, vua Bảo Đại thoái vị. Dân ta đã đánh đổ các xiềng xích thực dân gần một trăm năm nay để gây dựng nên nước Việt Nam độc lập. Dân ta lại đánh đổ chế độ quân chủ mấy mươi thế kỉ mà lập nên chế độ Dân chủ Cộng hòa.
(2) Bởi thế cho nên, chúng tôi, Lâm thời Chính phủ của nước Việt Nam mới, đại biểu cho toàn dân Việt Nam, tuyên bố thoát li hẳn quan hệ thực dân với Pháp, xóa bỏ hết những hiệp ước mà Pháp đã kí về nước Việt Nam, xóa bỏ tất cả mọi đặc quyền của Pháp trên đất nước Việt Nam.
(3) Toàn dân Việt Nam, trên dưới một lòng, kiên quyết chống lại âm mưu của bọn thực dân Pháp.
(4) Chúng tôi tin rằng các nước đồng minh đã công nhận những nguyên tắc dân tộc bình đẳng ở các hội nghị Tê-hê-răng và Cựu Kim Sơn, quyết không thể không công nhận quyền độc lập của dân Việt Nam.
(5) Một dân tộc đã gan góc chống ách nô lệ của Pháp hơn 80 năm nay, một dân tộc đã gan góc đứng về phe Đồng minh chống phát xít mấy năm nay, dân tộc đó phải được tự do! Dân tộc đó phải được độc lập!
(6) Vì những lẽ trên, chúng tôi, Chính phủ lâm thời của nước Việt Nam Dân chủ Cộng hòa, trịnh trọng tuyên bố với thế giới rằng:
(7) Nước Việt Nam có quyền hưởng tự do và độc lập, và sự thật đã thành một nước tự do, độc lập. Toàn thể dân tộc Việt Nam quyết đem tất cả tinh thần và lực lượng, tính mạng và của cải để giữ vững quyền tự do, độc lập ấy.
(Tuyên ngôn Độc lập – Hồ Chí Minh)
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Sông Mã xa rồi Tây Tiến ơi!
Nhớ về rừng núi, nhớ chơi vơi
Sài Khao sương lấp đoàn quân mỏi
Mường Lát hoa về trong đêm hơi
Dốc lên khúc khuỷu dốc thăm thẳm
Heo hút cồn mây súng ngửi trời
Ngàn thước lên cao ngàn thước xuống
Nhà ai Pha Luông mưa xa khơi
Anh bạn dãi dầu không bước nữa
Gục lên súng mũ bỏ quên đời!
Chiều chiều oai linh thác gầm thét
Đêm đêm Mường Hịch cọp trêu người
Nhớ ôi Tây Tiến cơm lên khói
Mai Châu mùa em thơm nếp xôi.
(Tây Tiến – Quang Dũng)
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 5
Dựa vào các thông tin sau đây để trả lời các câu hỏi từ câu 109 đến Câu 110.
"Đầu tháng 8-1945, quân Đồng minh tiến công mạnh mē vào các vị trí của quân đội Nhật Bản ở châu Á Thái Bình Dương. Để uy hiếp quân Nhật, ngày 6 và 9-8-1945, Mĩ đã ném hai quả bom nguyên tử xuống thành phố Hirôsima và Nagaxaki của Nhật Bản, huỷ diệt hai thành phố này và giết hại hàng vạn dân thường.
Ngày 8-8-1945, Liên Xô tuyên chiến với Nhật Bản. Ngày 9-8, quân đội Xô viết mở màn chiến dịch tổng công kích đạo quân Quan Đông của Nhật Bản ở Đông Bắc Trung Quốc.
Trước tình thế đó, Hội đồng tối cao chiến tranh và Nội các Nhật Bản họp, với sự tham gia của Nhật hoàng, thông qua quyết định đầu hàng. Giữa trưa 15-8-1945, Nhật hoàng tuyên bố đầu hàng Đồng minh không điều kiện trên sóng phát thanh của Nhật Bản.
Quân Nhật ở Đông Dương rệu rã. Chính phủ thân Nhật Trần Trọng Kim hoang mang. Điều kiện khách quan thuận lợi cho tổng khởi nghĩa đã đến.
Ngay từ ngày 13-8-1945, khi nhận được những thông tin về việc Nhật Bản sắp đầu hàng, Trung ương Đảng và Tống bộ Việt Minh lập tức thành lập Uỷ Ban Khởi nghĩa toàn quốc Đến 23 giờ cùng ngày, Uỷ Ban Khởi nghĩa toàn quốc Ban bố "Quân lệnh số 1", chính thức phát lệnh Tổng khởi nghĩa trong cả nước Từ ngày 14 đến ngày 15-8-1945, Hội nghị toàn quốc của Đảng họp ở Tân Trào (Sơn Dương-Tuyên Quang), thông qua kế hoạch lãnh đạo toàn dân Tổng khởi nghĩa và quyết định những vấn đề quan trọng về chính sách đối nội, đối ngoại sau khi giành được chính quyền.
Tiếp đó, từ ngày 16 đến ngày 17-8-1945, Đại hội Quốc dân được triệu tập ở Tân Trào. Đại hội tán thành chủ trương Tổng khởi nghĩa của Đảng, thông qua 10 chính sách của Việt Minh, cử ra Uỷ Ban Dân tộc giải phóng Việt Nam do Hồ Chí Minh làm Chủ tịch".
(Nguồn: SGK Lịch sử 12, NXB Giáo dục Việt Nam, 2023, trang 115).
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Đồ thị sau biểu diễn thể tích khí nitrogen thu được theo thời gian bằng phản ứng phân huỷ chất chứa nitrogen (hình bên). Dựa vào đồ thị ta thấy từ thời gian x (giây) đến y (giây) phản ứng xảy ra nhanh nhất, khi phản ứng kết thúc thì thu được z (\[c{m^3}\]) khí \({N_2}\). Các giá trị của x, y, z lần lượt là: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/07/blobid7-1721824237.png)