Trong không gian \[Oxyz,\] cho đường thẳng \(d:\frac{{x + 1}}{2} = \frac{y}{{ - 1}} = \frac{{z - 1}}{1}\) cắt mặt phẳng \(\left( P \right):x - 2y - z - 1 = 0\) tại điểm \[M.\] Mặt cầu \(\left( S \right)\) có tâm \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) với \(a > 0\) thuộc đường thẳng \(d\) và tiếp xúc với mặt phẳng \(\left( P \right)\) tại điểm \[A.\] Biết rằng diện tích tam giác \[IAM\] bằng \(12\sqrt 3 .\) Tổng \(a + b + c\) bằng

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 17) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

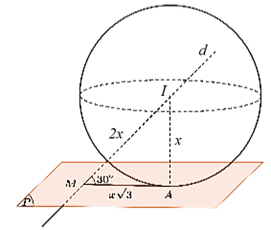
Media VietJack

Đường thẳng \(d\) có vectơ chỉ phương là \(\vec u = \left( {2\,;\,\, - 1\,;\,\,1} \right)\) và mặt phẳng \((P)\) có vectơ pháp tuyến là \(\vec n = \left( {1\,;\,\, - 2\,;\,\, - 1} \right).\)

Gọi \(\alpha \) là góc giữa đường thẳng \(d\) và mặt phẳng \((P)\) ta có \(\sin \alpha = \frac{{\left| {\vec n \cdot \vec u} \right|}}{{\left| {\vec n} \right| \cdot \left| {\vec u} \right|}} = \frac{1}{2} \Rightarrow \alpha = 30^\circ .\)

Đặt \(IA = x\) thì ta sẽ có \(MA = IA \cdot \cot 30^\circ = x\sqrt 3 .\)

Diện tích của tam giác \[IAM\] bằng:

\({S_{IAM}} = \frac{1}{2}IA \cdot AM = \frac{1}{2} \cdot x \cdot x\sqrt 3 = 12\sqrt 3 \Rightarrow x = \sqrt {24} .\)

Do \(I \in d \Rightarrow I\left( { - 1 + 2t\,;\,\, - t\,;\,\,1 + t} \right)\), điều kiện \( - 1 + 2t > 0 \Leftrightarrow t > \frac{1}{2}.\)

Khi đó \[d\left( {I;\,\,\left( P \right)} \right) = IA = \frac{{\left| { - 1 + 2t + 2t - \left( {1 + t} \right) - 1} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\left| {3t - 3} \right|}}{{\sqrt 6 }} = 2\sqrt 6 \]

\[ \Leftrightarrow 3\left| {t - 1} \right| = 12 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t - 1 = 4}\\{t - 1 = - 4}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{t = 5{\rm{ (TM) }}}\\{t = - 3{\rm{ (L) }}}\end{array}} \right.} \right.\].

Với \[t = 5 \Rightarrow I\left( {9\,;\,\, - 5\,;\,\,6} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 9}\\{b = - 5.}\\{c = 6}\end{array}} \right.\] Vậy \[a + b + c = 10.\]

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng

A. 3.

B. 5.

C. 10.

D. 2.

Lời giải

Ta có \(f'\left( x \right) = m \cdot \frac{1}{{2\sqrt {x - 1} }}\).

Do \(m \ne 0\) nên \(f'\left( x \right) \ne 0\) và có dấu không thay đổi \(\forall x \in \left( {1\,;\,\, + \infty } \right).\)

TH1: Nếu \(m > 0\) thì \(f'\left( x \right) > 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)

Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m.\)

Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)

\( \Leftrightarrow m + 2m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).

Do \(m > 0\) nên nhận \({m_2} = 5.\)

TH2: Nếu \(m < 0\) thì \(f'\left( x \right) < 0\,,\,\,\forall x \in \left[ {2;\,\,5} \right].\)

Do đó \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(5) = 2m\,;\,\,{\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = f(2) = m.\)

Suy ra \({\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10\)

\( \Leftrightarrow 2m + m = {m^2} - 10\)\( \Leftrightarrow {m^2} - 3m - 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{m_1} = - 2}\\{{m_2} = 5}\end{array}} \right.\).

Do \(m < 0\) nên nhận \({m_1} = - 2.\)

Vậy \({m_1} + {m_2} = 3.\) Chọn A.

Câu 2

Đọc đoạn trích sau đây và trả lời câu hỏi:

                                             Nếu Tổ quốc neo mình đầu sóng cả

                                             Những chàng trai ra đảo đã quên mình

                                             Một sắc chỉ về Hoàng Sa thuở trước

                                             Còn truyền đời con cháu mãi đinh ninh



                                             Nếu Tổ quốc nhìn từ bao mất mát

                                             Máu xương kia dằng dặc suốt ngàn đời

                                             Hồn dân tộc ngàn năm không chịu khuất

                                             Dáng con tàu vẫn hướng mãi ra khơi.

(Nguyễn Việt Chiến, Tổ quốc nhìn từ biển, NXB Phụ nữ, 2015)

Nhân vật trữ tình đã gửi gắm cảm xúc, tâm tư gì vào đoạn thơ?

A. Những băn khoăn, trăn trở trước sự xâm lược của giặc ngoại xâm đối với biển đảo quê hương từ xưa đến nay.

B. Những suy ngẫm, tự hào về lịch sử dân tộc, trách nhiệm của mỗi con người trong công cuộc bảo vệ Tổ quốc hôm nay.

C. Sự tự hào, ngợi ca đối với vẻ đẹp và sự giàu có của biển đảo quê hương.

D. Nỗi xót xa, đau đớn trước những tấm gương anh hùng đã ngã xuống để bảo vệ biển đảo quê hương.

Lời giải

Học sinh đọc ngữ liệu, căn cứ vào các hình ảnh “chàng trai ra đảo đã quên mình, máu xương kia dằng dặc suốt ngàn đời, hồn dân tộc ngàn năm không chịu khuất” để thấy những suy ngẫm, chiêm nghiệm của tác giả, đồng thời cùng với đó là sự trân trọng, tự hào đối với lịch sử bảo vệ biển đảo, bảo vệ Tổ quốc. Học sinh căn cứ tiếp vào câu “Dáng con tàu vẫn hướng mãi ra khơi” để thấy sự tiến về phía trước của thế hệ tương lai, thể hiện trách nhiệm của thế hệ trẻ đối với công cuộc bảo vệ Tổ quốc. Chọn B.

Câu 3