Câu hỏi:
13/07/2024 2,610
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.
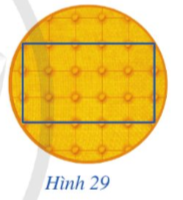
Mặt trên của tấm đệm có dạng hình tròn ở Hình 29 gợi nên hình ảnh đường tròn ngoại tiếp hình chữ nhật. Biết hình chữ nhật đó có chiều rộng, chiều dài lần lượt là 3 dm, 5 dm. Tính độ dài đường kính mặt trên của tấm đệm, từ đó tính diện tích mặt trên của tấm đệm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
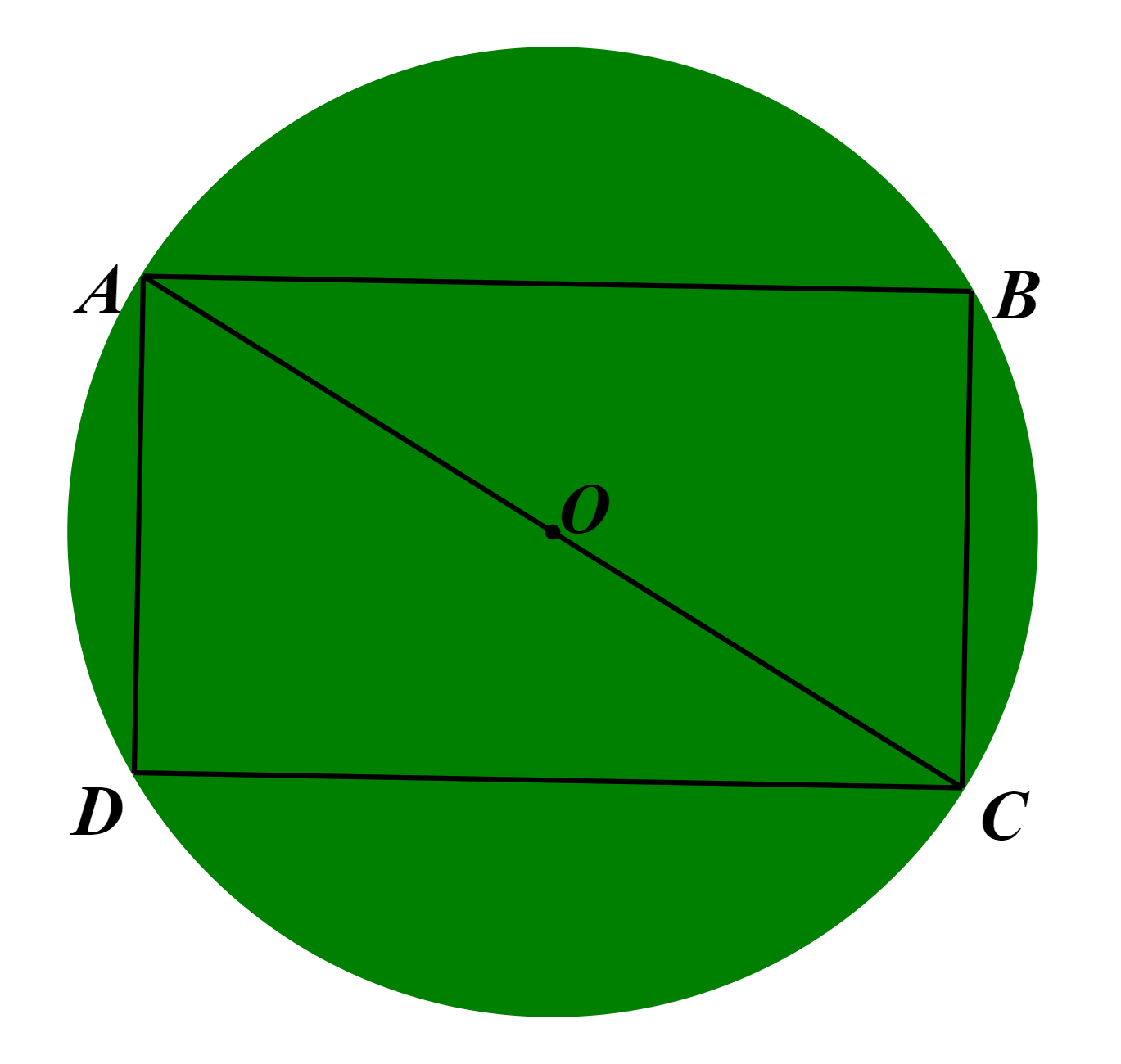
Giả sử hình chữ nhật ABCD có AD = BC = 3 dm, AB = CD = 5 dm có đường tròn (O) là đường tròn ngoại tiếp.
Do đó tâm O là giao điểm hai đường chéo và đường chéo AC là đường kính của đường tròn (O).
Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:
AC2 = AD2 + DC2 = 52 + 32 = 34.
Suy ra 
Do đó bán kính của đường tròn (O) là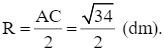 
Diện tích hình tròn bán kính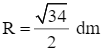 
là:
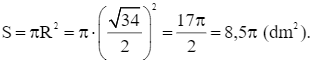
Vậy mặt trên của tấm nệm có độ dài đường kính là 
dm và diện tích bằng 8,5π dm2.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
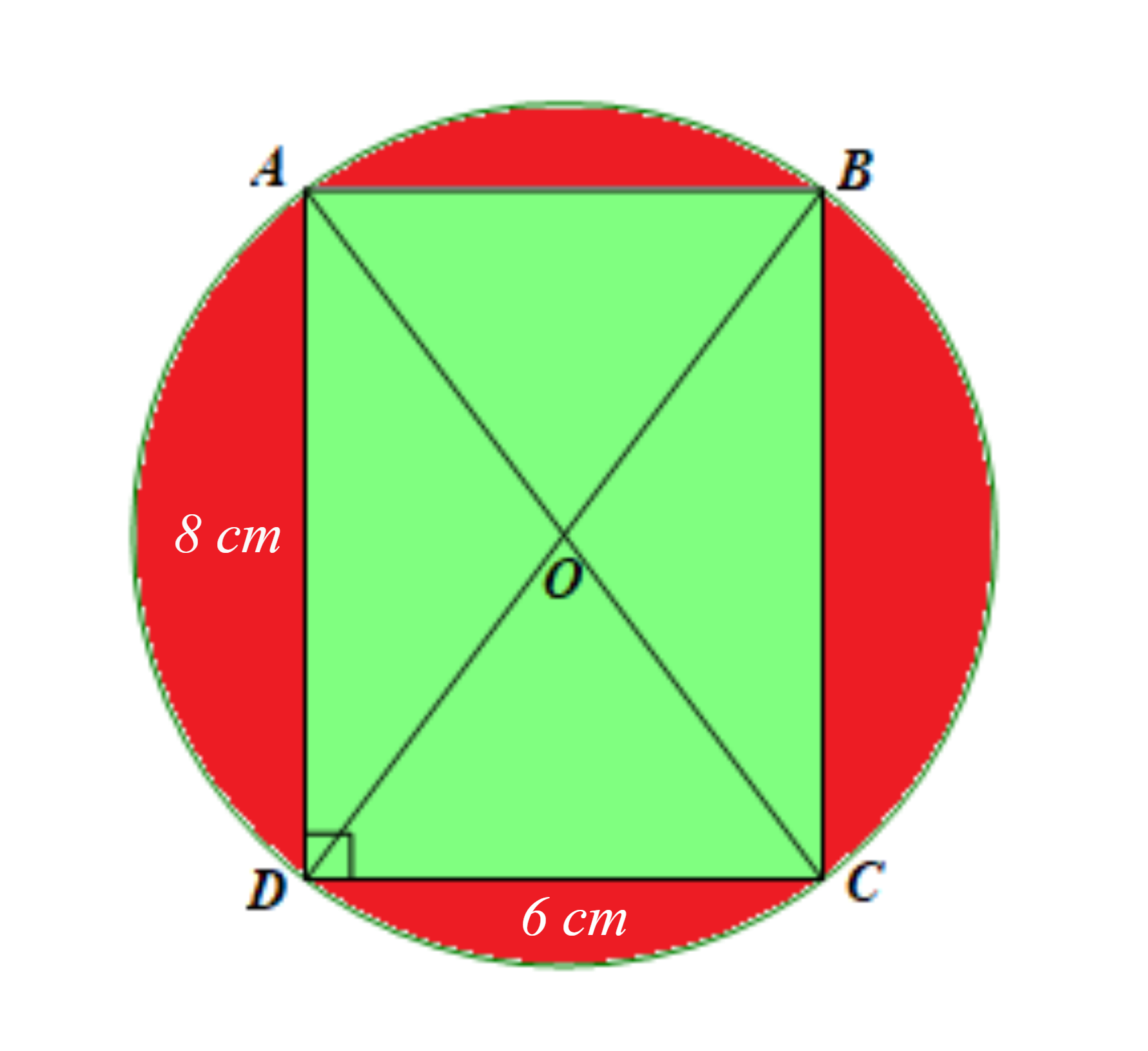
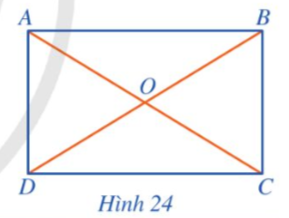
Giả sử hình chữ nhật ABCD nội tiếp đường tròn (O) có AB = CD = 6 cm và AD = BC = 8 cm.
Khi đó đường chéo AC là đường kính của đường tròn (O).
Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:
AC2 = AD2 + DC2 = 82 + 62 = 100.
Suy ra AC = 10 cm.
Do đó bán kính của đường tròn (O) là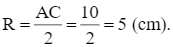 
Diện tích hình tròn bán kính R = 5 cm là:
S1 = πR2 = π.52 = 25π (cm2).
Diện tích hình chữ nhật ABCD là:
S2 = AD.DC = 8.6 = 48 (cm2).
Diện tích phần được tô màu đỏ là:
S = S1 – S2 = 25π – 48 (cm2) ≈ 30,5 (cm2) với π ≈ 3,14.
Lời giải
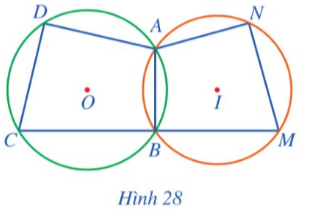
Ở Hình 28:
⦁ đường tròn (O) ngoại tiếp tứ giác ABCD vì đường tròn (O) đi qua các đỉnh A, B, C, D của tứ giác ABCD;
⦁ đường tròn (I) ngoại tiếp tứ giác ABMN vì đường tròn (I) đi qua các đỉnh A, B, M, N của tứ giác ABMN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo