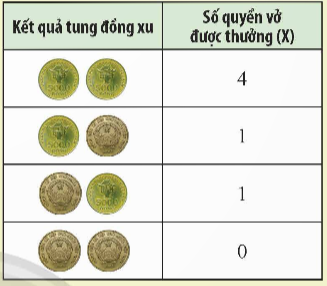
Kết quả khảo sát cân nặng (làm tròn đến 100 g) của 50 trái sầu riêng trong một lô hàng A được tổng hợp ở bảng sau:

Chọn ngẫu nhiên 1 trái sầu riêng trong lô hàng A và gọi X là cân nặng (làm tròn đến 100 g) của trái sầu riêng đó. Hãy tính kì vọng và độ lệch chuẩn của X.
Kết quả khảo sát cân nặng (làm tròn đến 100 g) của 50 trái sầu riêng trong một lô hàng A được tổng hợp ở bảng sau:

Quảng cáo
Trả lời:
Do có 6 trái sầu riêng có cân nặng 2 400 g nên số kết quả thuận lợi cho biến cố “X bằng 2 400” là 6. Xác suất của biến cố “X bằng 2 400” là 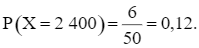
Tương tự, ta có 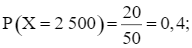
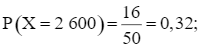
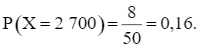
Ta có bảng phân bố xác suất của X là:
|
X |
2 400 |
2 500 |
2 600 |
2 700 |
|
P |
0,12 |
0,4 |
0,32 |
0,16 |
Kì vọng của X là:
E(X) = 2 400 . 0,12 + 2 500 . 0,4 + 2 600 . 0,32 + 2 700 . 0,16 = 2 552.
Phương sai của X là:
V(X) = 2 4002 . 0,12 + 2 5002 . 0,4 + 2 6002 . 0,32 + 2 7002 . 0,16 – 2 5522 = 8 096.
Độ lệch chuẩn của X là:
![]()
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tập hợp các giá trị có thể của X là: {0; 1; 2}.
Xác suất bạn Dung không được thưởng bóng bay là:
P(X = 0) = 1 – P(X = 1) – P(X = 2) = 1 – 0,2 – 0,1 = 0,7.
Vậy ta có bảng phân bố xác suất cho biến ngẫu nhiên rời rạc X như sau:
|
X |
0 |
1 |
2 |
|
P |
0,7 |
0,2 |
0,1 |
Lời giải
Gọi X là số tiền thu về cho một lần chơi.
Vì trong một lần chơi thì số tiền thu về có thể là:
⦁ –1 000 đồng nếu không có quả bóng nào cùng số với hộp;
⦁ 1 000 đồng nếu có đúng một quả bóng cùng số với hộp;
⦁ 5 000 đồng nếu cả ba quả bóng đều cùng số với hộp.
Vậy tập giá trị của X là: {–1 000; 1 000; 5 000}.
Tổng số kết quả có thể xảy ra khi đặt 3 quả bóng vào 3 cái hộp là: n(Ω) = 3! = 6.
– Biến cố “X bằng –1 000” xảy ra khi không có quả bóng nào cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng –1 000” là: 2 . 1 . 1 = 2.
Xác suất của biến cố “X bằng –1 000” là: 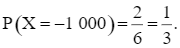
– Biến cố “X bằng 1 000” xảy ra khi có đúng một quả bóng cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng 1 000” là: (1 . 1 . 1) . 3 = 3.
Xác suất của biến cố “X bằng 1 000” là: 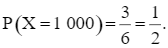
– Biến cố “X bằng 5 000” xảy ra khi cả ba quả bóng đều cùng số với hộp. Số kết quả thuận lợi cho biến cố “X bằng 5 000” là: 1.
Xác suất của biến cố “X bằng 5 000” là: 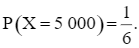
Ta có bảng phân bố xác suất của X là:
|
X |
–1 000 |
1 000 |
5 000 |
|
P |
|
|
|
Kì vọng của X là:
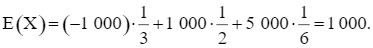
Ta thấy E(X) > 0 nên nếu so sánh về mặt trung bình thì người chơi có lợi hơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.