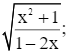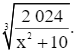Câu hỏi:
12/07/2024 977
Một chất điểm di chuyển từ đỉnh A’ đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?
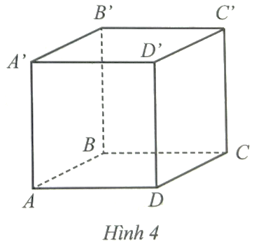
Một chất điểm di chuyển từ đỉnh A’ đến đỉnh C trên bề mặt của hình lập phương ABCD.A’B’C’D’ có độ dài cạnh 1 dm (Hình 4). Quãng đường ngắn nhất mà chất điểm đó di chuyển là bao nhiêu decimét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử chất điểm đó di chuyển qua các mặt ABB’A’ và BCC’B’ của hình lập phương (các trường hợp khác tương tự).
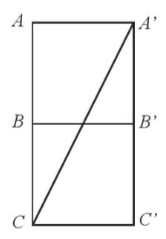
Hình vẽ trên là hình khai triển của các mặt ABB’A’ và BCC’B’.
Do tam giác AA’C vuông tại A nên theo định lí Pythagore, ta có:
A’C2 = AA’ + AC2
Suy ra A’C2 = AA’2 + (AB + BC)2 = 12 + (1 + 1)2 = 5.
Do đó 
Vậy quãng đường ngắn nhất mà chất điểm đó di chuyển là 
dm.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Điều kiện xác định biểu thức B là: 5x + 2 ≥ 0 hay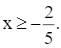 
Khi đó, ta có 
nên 
Suy ra 
hay B ≤ 2 024.
Vậy giá trị lớn nhất của biểu thức B là 2 024 khi 5x + 2 = 0 hay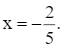 
Lời giải
Biểu thức 
xác định khi x + 2 024 ≥ 0 hay x ≥ ‒2 024.
xác định khi x + 2 024 ≥ 0 hay x ≥ ‒2 024.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận