Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng tính đến ngày 30/9/2021 lần lượt có số đo là bao nhiêu độ?
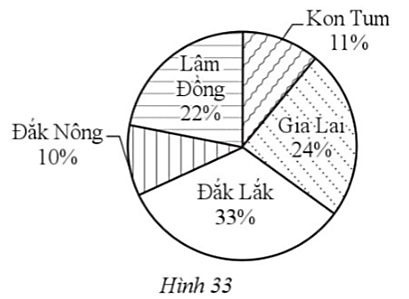
Biểu đồ hình quạt tròn ở Hình 33 biểu diễn số lớp học cấp trung học cơ sở của năm tỉnh Tây Nguyên tính đến ngày 30/9/2021 (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng tính đến ngày 30/9/2021 lần lượt có số đo là bao nhiêu độ?

Câu hỏi trong đề: Giải SBT Toán 9 Cánh Diều Bài 4. Góc ở tâm, góc nội tiếp !!
Quảng cáo
Trả lời:
Do số lớp học cấp trung học cơ sở của tỉnh Kon Tum chiếm 11% tổng số lớp học nên số đo cung tương ứng bằng 11% số đo của cung cả đường tròn. Vì thế, số đo cung này bằng
Tương tự, ta cũng tính được số đo của các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng.
Vậy các cung tương ứng với phần biểu diễn số lớp học cấp trung học cơ sở của các tỉnh Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng tính đến ngày 30/9/2021 lần lượt có số đo là: 39,6°; 86,4°; 118,8°; 36°; 79,2°.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
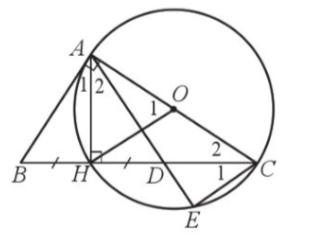
a) Xét ∆ABH và ∆ADH có:
BH = HD (do H là trung điểm của BD);
Cạnh AH chung
Do đó ∆ABH = ∆ADH (hai cạnh góc vuông).
Suy ra
Mà (vì cùng phụ với và (hai góc nội tiếp cùng chắn cung EH)
Suy ra
Vậy CH là tia phân giác của góc ACE.
b) Xét đường tròn (O) có và lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung AH nên
Mà (vì CH là tia phân giác của góc ACE)
Suy ra mà hai góc này ở vị trí đồng vị
Do đó OH // CE.
Lời giải

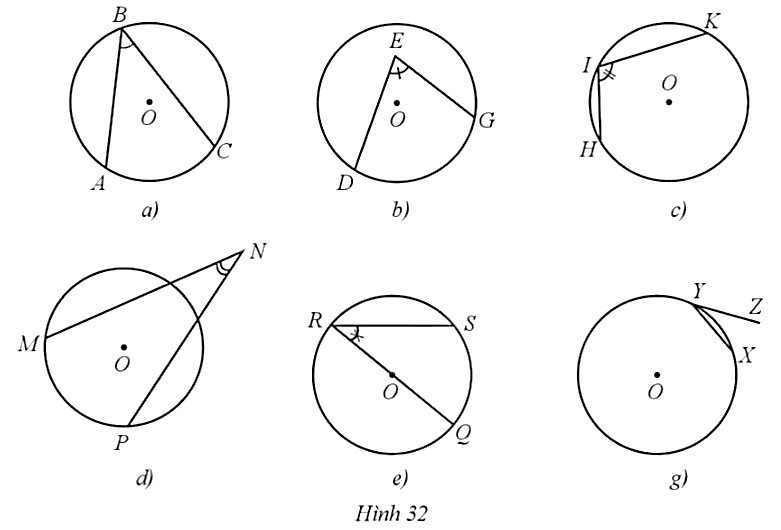
a) (Hình a) Vì MA, MB là các tiếp tuyến của đường tròn (O) nên MA ⊥ OA và MB ⊥ OB.
Xét tứ giác OAMB có:
Suy ra
Do đó số đo cung nhỏ AB bằng số đo của góc ở tâm AOB, bằng 140° và số đo cung lớn AB bằng 360° ‒ 140° = 220°.
b) (Hình b) Do số đo cung nhỏ AB bằng 120° suy ra
Lại có MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M nên MA = MB và OM là tia phân giác của góc AOB nên
Do tam giác OAM vuông tại A nên
Xét ∆OAM và ∆OBM có: OA = OB; MA = MB; OM là cạnh chung
Do đó ∆OAM = ∆OBM (c.c.c) nên S∆OAM = S∆OAM
Suy ra SOAMB = S∆OAM + S∆OBM = 2SOAM.
Vậy (đơn vị diện tích).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.