Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính băng 9 , tính thể tích V của khối chóp có thể tích lớn nhất.
Đáp án: ……….
Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính băng 9 , tính thể tích V của khối chóp có thể tích lớn nhất.
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử khối chóp đó là \[S.ABCD.\]
Ta có \(R = \frac{{S{A^2}}}{{2SH}} = 9 \Rightarrow \frac{{S{H^2} + A{H^2}}}{{SH}} = 18 \Leftrightarrow A{H^2} = 18 \cdot SH - S{H^2}\)
Mặt khác \[V = \frac{1}{3}SH \cdot {S_{ABCD}} = \frac{1}{3}SH \cdot \frac{{A{C^2}}}{2}\]
\[ = \frac{2}{3}SH \cdot A{H^2} = \frac{2}{3}SH \cdot \left( {18 \cdot SH - S{H^2}} \right).\]
Xét hàm số
\(f\left( t \right) = \frac{2}{3}{t^2}\left( {18 - t} \right) = \frac{8}{3} \cdot \left[ {\frac{t}{2} \cdot \frac{t}{2} \cdot \left( {18 - x} \right)} \right]\)\( \le \frac{8}{3} \cdot {\left( {\frac{{t + 18 - t}}{3}} \right)^3} = \frac{8}{3} \cdot {\left( {\frac{{18}}{3}} \right)^3} = 576\,\,\,\left( {0 < t < 18} \right).\)
Dấu xảy ra khi và chỉ khi \(\frac{t}{2} = 18 - t \Leftrightarrow t = 12.\)
Vậy thể tích của khối chóp \[S.ABCD\] đạt giá trị lớn nhất là 576 khi và chỉ khi \(SH = 12.\)
Đáp án: 576.
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Diện tích miếng đất là \({S_1} = \pi {R^2} = 25\pi \left( {{{\rm{m}}^2}} \right)\)
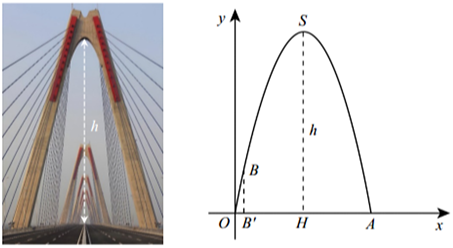
Chọn hệ trục tọa độ \[Oxy\] như hình vẽ.
Ta có phương trình của đường tròn biên là \({x^2} + {y^2} = 25\) nên\[R = 5\,,\,\,AH = 3 \Rightarrow OH = 4.\]
Phương trình của cung tròn nhỏ là \(y = \sqrt {25 - {x^2}} \), với \(4 \le x \le 5.\)
Diện tích phần đất trồng là \({S_2} = 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} \,\,\left( {\;{{\rm{m}}^2}} \right)\)
Diện tích phần đất trồng cây là \(S = {S_1} - {S_2} = 25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} \,\,\left( {\;{{\rm{m}}^2}} \right).\)
Số tiền thu được là \(T = 100S = 100\left( {25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} } \right) \approx 7\,\,445\) (nghìn đồng).
Đáp án: 7445.
Lời giải
Gọi chiều rộng của bể là \(3x\,\,(\;{\rm{m}}).\)
Ta có chiều dài bể là \(4x\,\,(\;{\rm{m}})\) và chiều cao của bể là \(\frac{2}{{3{x^2}}}\,\,({\rm{m}}).\)
Khi đó tổng diện tích bề mặt xây là
\(T = \left( {3x + 4x} \right) \cdot 2 \cdot \frac{2}{{3{x^2}}} + 2 \cdot 3x \cdot 4x - \frac{2}{9} \cdot 3x \cdot 4x\)\( = \frac{{28}}{{3{x^2}}} + \frac{{64{x^2}}}{3} \ge 2 \cdot \sqrt {\frac{{28}}{{3{x^2}}} \cdot \frac{{64{x^2}}}{3}} = \frac{{32\sqrt 7 }}{3}\,\,\left( {\;{{\rm{m}}^2}} \right)\).
Chi phí thấp nhất mà ông Nam phải chi trả để xây dựng bể nước là:
\(T \cdot 980\,\,000 \ge \frac{{32\sqrt 7 }}{3} \cdot 980\,\,000 \approx 27\,\,657\,\,000\) (đồng). Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo