Đọc đoạn trích sau và trả lời câu hỏi:

Từ ngã ba Tuần, sông Hương theo hướng nam bắc qua điện Hòn Chén; vấp Ngọc Trản, nó chuyển hướng sang tây bắc, vòng qua thềm đất bãi Nguyệt Biều, Lương Quán rồi đột ngột vẽ một hình cung thật tròn về phía đông bắc, ôm lấy chân đồi Thiên Mụ, xuôi dần về Huế. Từ Tuần về đây, sông Hương vẫn đi trong dư vang của Trường Sơn, vượt qua một lòng vực sâu dưới chân núi Ngọc Trản để sắc nước trở nên xanh thẳm, và từ đó nó trôi đi giữa hai dãy đồi sừng sững như thành quách, với những điểm cao đột ngột như Vọng Cảnh, Tam Thai, Lựu Bảo mà từ đó, người ta luôn luôn nhìn thấy dòng sông mềm như tấm lụa, với những chiếc thuyền xuôi ngược chỉ bé vừa bằng con thoi.

(Ai đã đặt tên cho dòng sông? – Hoàng Phủ Ngọc Tường)

Những biện pháp tu từ nghệ thuật nào được sử dụng trong đoạn trích?

A. Nhân hóa và so sánh.

B. Điệp từ và điệp ngữ.

C. So sánh và ẩn dụ.

D. Hoán dụ và nhân hóa.

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 27) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Biện pháp nhân hóa và so sánh:

+ Nhân hóa được thể hiện qua các từ ngữ: chuyển hướng, vòng qua, vẽ một hình cung, ôm lấy, xuôi dần,...

+ So sánh được thể hiện qua các câu văn: và từ đó nó trôi đi giữa hai dãy đồi sừng sững như thành quách, người ta luôn luôn nhìn thấy dòng sông mềm như tấm lụa, với những chiếc thuyền xuôi ngược chỉ bé vừa bằng con thoi.

→ Chọn A.

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một người có miếng đất hình tròn có bán kính bằng 5 m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn đồng. Tuy nhiên cần có 1 khoảng trống để dựng một cái chòi và để đồ dùng nên người này bớt lại 1 phần đất nhỏ không trồng cây (phần màu trẳng như hình vẽ), trong đó AB = 6m Hỏi khi thu hoạch cây thì người này thu được bao nhiêu nghìn đồng (làm tròn đến hàng nghìn)?
Đáp án: ……….

Xem đáp án

Lời giải

Một người có miếng đất hình tròn có bán kính bằng 5 m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn đồng. Tuy nhiên cần có 1 khoảng trống đ (ảnh 1)

Diện tích miếng đất là \({S_1} = \pi {R^2} = 25\pi \left( {{{\rm{m}}^2}} \right)\)

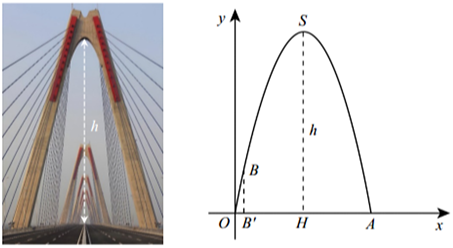
Chọn hệ trục tọa độ \[Oxy\] như hình vẽ.

Ta có phương trình của đường tròn biên là \({x^2} + {y^2} = 25\) nên\[R = 5\,,\,\,AH = 3 \Rightarrow OH = 4.\]

Phương trình của cung tròn nhỏ là \(y = \sqrt {25 - {x^2}} \), với \(4 \le x \le 5.\)

Diện tích phần đất trồng là \({S_2} = 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} \,\,\left( {\;{{\rm{m}}^2}} \right)\)

Diện tích phần đất trồng cây là \(S = {S_1} - {S_2} = 25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} \,\,\left( {\;{{\rm{m}}^2}} \right).\)

Số tiền thu được là \(T = 100S = 100\left( {25\pi - 2\int\limits_4^5 {\sqrt {25 - {x^2}} dx} } \right) \approx 7\,\,445\) (nghìn đồng).

Đáp án: 7445.

Câu 2

Cầu Nhật Tân bắc qua sông Hồng được xem là chiếc cầu dây văng dài nhất Việt Nam năm 2022. Cầu có 5 trụ tháp chính kết nối các nhịp dây văng đỡ toàn bộ phần chính của cây cầu, cũng là để tượng trưng cho 5 cửa ô cổ kính của Hà Nội. Mỗi trụ tháp được kiến trúc tạo dáng mĩ thuật phía trong bằng đường cong tựa như một parabol.

Giả sử rằng mặt trong của trụ cầu là một parabol như vẽ, biết độ rộng của mặt đường khoảng \[43{\rm{ }}m.\] Một người đã dùng dây dọi (không giãn) gắn lên thành trụ cầu ở vị trí \[B\] và điều chỉnh độ dài dây dọi để quả nặng vừa chạm đất (khi lặng gió), sau đó đo được chiều dài đoạn dây dọi sử dụng là \[1,87{\rm{ }}m\] và khoảng cách từ chân trụ cầu đến quả nặng là \[20{\rm{ }}cm.\] Nếu dùng dữ liệu tự thu thập được và tính toán theo cách ở trên thì người này sẽ ước tính được độ cao từ đỉnh vòm phía trong một trụ của cầu Nhật Tân tới mặt đường là bao nhiêu mét (làm tròn đến hàng đơn vị)?

Đáp án: ……….

Xem đáp án

Lời giải

Đồ thị hàm số bậc hai \(y = a{x^2} + bx + c\) đi qua gốc tọa độ \(O\left( {0\,;\,\,0} \right)\) nên \(c = 0.\)

Suy ra công thức hàm số là \(a{x^2} + bx.\)

Mặt khác đồ thị hàm số qua hai điểm \(A\left( {43\,;\,\,0} \right),\,\,B\left( {0,2\,;\,\,1,87} \right)\) nên ta có hệ phương trình:

\[\left\{ {\begin{array}{*{20}{l}}{a \cdot {{\left( {0,2} \right)}^2} + b \cdot 0,2 = 1,87}\\{a \cdot {{43}^2} + b \cdot 43 = 0}\end{array}} \right.\]

Suy ra \(a = - \frac{{187}}{{856}};\,\,b = \frac{{8041}}{{856}}\) nên có hàm số \(y = - \frac{{187}}{{856}}{x^2} + \frac{{8041}}{{856}}x.\)

Hình chiếu của đỉnh \(S\) trên trục hoành là \(H\) nên

\({y_S} = f\left( {{x_S}} \right) = f\left( {{x_H}} \right) = f\left( {\frac{{{x_A}}}{2}} \right) = f\left( {\frac{{43}}{2}} \right) \approx 101\,\,(m).\)

Vậy độ cao từ đỉnh vòm phia trong một trụ của cầu Nhật Tân tới mặt đường là khoảng \(101\;\,\,{\rm{m}}.\)

Đáp án: 101.

Câu 3