Câu hỏi:
06/08/2024 183
Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ có khối lượng m. Ban đầu vật m được giữ ở vị trí để lò xo bị nén 9 cm. Vật M có khối lượng bằng một nửa khối lượng vật m, nằm sát m. Thả nhẹ m để hai vật chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên, khoảng cách giữa hai vật m và M có giá trị bằng bao nhiêu cm? Làm tròn đến chữ số thập phân thứ nhất.
Đáp án: ……….
Một con lắc lò xo đặt trên mặt phẳng nằm ngang gồm lò xo nhẹ có một đầu cố định, đầu kia gắn với vật nhỏ có khối lượng m. Ban đầu vật m được giữ ở vị trí để lò xo bị nén 9 cm. Vật M có khối lượng bằng một nửa khối lượng vật m, nằm sát m. Thả nhẹ m để hai vật chuyển động theo phương của trục lò xo. Bỏ qua mọi ma sát. Ở thời điểm lò xo có chiều dài cực đại lần đầu tiên, khoảng cách giữa hai vật m và M có giá trị bằng bao nhiêu cm? Làm tròn đến chữ số thập phân thứ nhất.
Đáp án: ……….
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi hệ vật chuyển động từ vị trí biên ban đầu đến VTCB:
CLLX \((m + M = 1,5m)\):\({v_{\max }} = A{\rm{\omega }} = A\sqrt {\frac{k}{{1,5m}}} {\rm{. }}\)
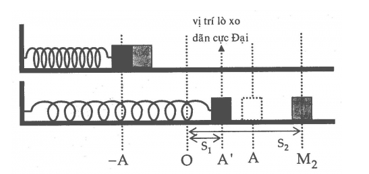
Khi đến VTCB, hai vật tách khỏi nhau do m bắt đầu chuyển động chậm dần, lúc này M chuyển động thẳng đều với vận tốc \({{\rm{v}}_{\max }}\) ở trên.
Xét CLLX có vật m (vận tốc cực đại không thay đồi):
\({{\rm{v}}_{\max }} = {{\rm{A}}^\prime }{{\rm{\omega }}^\prime } = {{\rm{A}}^\prime }\sqrt {\frac{{\rm{k}}}{{\rm{m}}}} = {\rm{A}}\sqrt {\frac{{\rm{k}}}{{1,5\;{\rm{m}}}}} \Rightarrow {{\rm{A}}^\prime } = \frac{{\rm{A}}}{{\sqrt {1,5} }} = \frac{9}{{\sqrt {1,5} }}\;{\rm{cm}}\)
Từ khi tách nhau (qua VTCB) đến khi lò xo có chiều dài cực đại thì m đến vị trí biên Aˊ, thời gian dao động là \(\Delta {\rm{t}} = \frac{{\rm{T}}}{4} = \frac{{2{\rm{\pi }}}}{{4{{\rm{\omega }}^\prime }}} = \frac{{\rm{\pi }}}{{2{{\rm{\omega }}^\prime }}};\) với \({{\rm{\omega }}^\prime } = \sqrt {\frac{{\rm{k}}}{{\rm{m}}}} = {\rm{\omega }}\sqrt {1,5} \Rightarrow \Delta {\rm{t}} = \frac{\pi }{{{\rm{\omega }}.2\sqrt {1,5} }}\).
Trong thời gian này, \({\rm{M}}\) đi được quãng đường: \({\rm{s}} = {{\rm{v}}_{\max }} \cdot \Delta t = \omega {\rm{A}} \cdot \frac{\pi }{{\omega \cdot 2\sqrt {1,5} }} = \frac{{4,5\pi }}{{\sqrt {1,5} }}\;{\rm{cm}}\)
Khoảng cách hai vật: \(\Delta d = s - {A^\prime } \approx 4,2\;{\rm{cm}}{\rm{.}}\) Đáp án. 4,2
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \[f'\left( 1 \right) = 3 \Rightarrow a + b = 3\]. (1)
Hàm số có đạo hàm liên tục trên khoảng \[\left( {0\,;\,\, + \infty } \right)\], các điểm \(x = 1,x = \frac{1}{2}\) đều thuộc \((0; + \infty )\) nên
\(f(x) = \int {f'} (x){\rm{d}}x = \int {\left( {a{x^2} + \frac{b}{{{x^3}}}} \right)} \,\,{\rm{d}}x = \frac{{a{x^3}}}{3} - \frac{b}{{2{x^2}}} + C.\)
• \(f\left( 1 \right) = 2 \Leftrightarrow \frac{a}{3} - \frac{b}{2} + C = 2\). (2)
• \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}} \Rightarrow \frac{a}{{24}} - 2b + C = - \frac{1}{{12}}\). (3).
Từ (1), (2) và (3) ta được hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = 3}\\{\frac{a}{3} - \frac{b}{2} + C = 2}\\{\frac{a}{{24}} - 2b + C = - \frac{1}{{12}}}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2}\\{b = 1}\\{C = \frac{{11}}{6}}\end{array} \Rightarrow 2a + b = 2 \cdot 2 + 1 = 5.} \right.} \right.\)
Chọn C.
Lời giải
Gọi I là tâm của mặt cầu \((S),\,\,I \in d \Rightarrow I\left( {1 + t\,;\,\,1 + 2t\,;\,\, - 2 + t} \right).\)
\( \Rightarrow \overrightarrow {AI} = \left( {3 + t\,;\,\, - 3 + 2t\,;\,\, - 3 + t} \right)\,;\,\,\overrightarrow {BI} = \left( { - 1 + t\,;\,\,1 + 2t\,;\,\, - 5 + t} \right)\)
Vì (S) đi qua \[A,\,\,B\] nên ta có \(IA = IB \Leftrightarrow I{A^2} = I{B^2}\)
\[ \Leftrightarrow {(3 + t)^2} + {\left( { - 3 + 2t} \right)^2} + {\left( { - 3 + t} \right)^2} = {\left( { - 1 + t} \right)^2} + {\left( {1 + 2t} \right)^2} + {\left( { - 5 + t} \right)^2}\]
\( \Leftrightarrow 4t = 0 \Leftrightarrow t = 0 \Rightarrow \overrightarrow {IA} = \left( {3\,;\,\, - 3\,;\,\, - 3} \right).\)
Vậy bán kính mặt cầu \[(S)\] là \[R = IA = \sqrt {{3^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} = 3\sqrt 3 .\] Chọn A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Top 10 đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2023 - 2024 có đáp án (Đề 7)
Nhắn tin Zalo