Câu hỏi:
06/08/2024 198
Trong thí nghiệm Young về giao thoa ánh sáng đơn sắc với bước sóng \(\lambda \), khoảng cách giữa hai khe là 1,0 mm. Vẫn giao thoa được quan sát qua một kính lúp có tiêu cự 5 cm đặt cách mặt phẳng hai khe một khoảng L = 65 cm. Một người có mặt bình thường đặt mắt sát kính lúp và quan sát hệ vân trong trạng thái không điều tiết thì thấy góc trông khoảng vân là 20,5'. Bước sóng của ánh sáng dùng trong thí nghiệm trên là bao nhiêu?
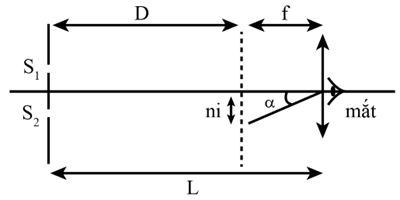
Trong thí nghiệm Young về giao thoa ánh sáng đơn sắc với bước sóng \(\lambda \), khoảng cách giữa hai khe là 1,0 mm. Vẫn giao thoa được quan sát qua một kính lúp có tiêu cự 5 cm đặt cách mặt phẳng hai khe một khoảng L = 65 cm. Một người có mặt bình thường đặt mắt sát kính lúp và quan sát hệ vân trong trạng thái không điều tiết thì thấy góc trông khoảng vân là 20,5'. Bước sóng của ánh sáng dùng trong thí nghiệm trên là bao nhiêu?
Đáp án chính xác
Quảng cáo
Trả lời:
Giải bởi Vietjack
Góc trông vật = góc hợp giữa 2 tia sáng từ 2 đầu mút của vật tới quang tâm của mắt.
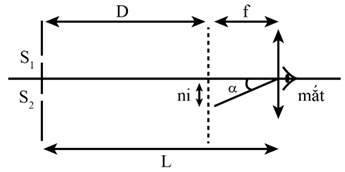
Góc trông khoảng vân \({\rm{\alpha }} = \tan {\rm{\alpha }} = \frac{{{\rm{ ni }}}}{{\rm{f}}}\)(với n = 1).
Khi quan sát khoảng vân qua kính lúp, mắt đặt sát kính lúp và muốn quan sát trong trạng thái không điều tiết (với mắt bình thường) thì ảnh của hệ vân qua kính lúp phải ở vô cùng, tức là khi đó hệ vân giao thoa sẽ nằm tại tiêu diện vật của kính lúp. Nói cách khác, tiêu diện vật của kính lúp đóng vai trò là màn ảnh của hệ giao thoa.
Theo đề bài: \({\rm{D}} = {\rm{L}} - {\rm{f}} = 60(\;{\rm{cm}})\)
Do\[{\rm{\alpha }} \ll \,\, \Rightarrow \tan {\rm{\alpha }} \approx {\rm{\alpha }} \Rightarrow {\rm{\alpha }} = \frac{i}{f} \Rightarrow {\rm{i}} = {\rm{f\alpha }} = \frac{{50.20,5.3,14}}{{60.180}} \approx 0,3\;{\rm{mm}} \Rightarrow \lambda = \frac{{{\rm{ia}}}}{{\rm{D}}} = 500\;{\rm{nm}}{\rm{.}}\] Chọn B.
Nhà sách vietjack
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số \(f\left( x \right)\) thỏa mãn các điều kiện \(f'\left( x \right) = a{x^2} + \frac{b}{{{x^3}}},\,\,f'(1) = 3,\,\,f\left( 1 \right) = 2\) và \(f\left( {\frac{1}{2}} \right) = - \frac{1}{{12}}.\) Khi đó, giá trị của \(2a + b\) bằng
Xem đáp án »
19/06/2024
9,082
Câu 2:
Trong không gian \[Oxyz,\] cho hai điểm \(A\left( { - 2\,;\,\,4\,;\,\,1} \right),\,\,B\left( {2\,;\,\,0\,;\,\,3} \right)\) và đường thẳng \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 1 + 2t}\\{z = - 2 + t}\end{array}} \right..\) Gọi \((S)\) là mặt cầu đi qua \[A,\,\,B\] và có tâm thuộc đường thẳng \[d.\] Bán kính mặt cầu \((S)\) bằng
Xem đáp án »
19/06/2024
4,492
Câu 3:
Trong không gian \[Oxyz,\] cho hai điểm \[A\left( {3\,;\,\,1\,;\,\,2} \right),\,\,B\left( { - 3\,;\,\, - 1\,;\,\,0} \right)\] và mặt phẳng \((P):x + y + 3z - 14 = 0.\) Điểm \(M\) thuộc mặt phẳng \((P)\) sao cho \(\Delta MAB\) vuông tại \[M.\] Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {Oxy} \right).\)
Trong không gian \[Oxyz,\] cho hai điểm \[A\left( {3\,;\,\,1\,;\,\,2} \right),\,\,B\left( { - 3\,;\,\, - 1\,;\,\,0} \right)\] và mặt phẳng \((P):x + y + 3z - 14 = 0.\) Điểm \(M\) thuộc mặt phẳng \((P)\) sao cho \(\Delta MAB\) vuông tại \[M.\] Tính khoảng cách từ điểm \(M\) đến mặt phẳng \(\left( {Oxy} \right).\)
Xem đáp án »
11/07/2024
2,766
Câu 4:
Đọc đoạn trích sau và trả lời câu hỏi:
Tiếng ai tha thiết bên cồn
Bâng khuâng trong dạ, bồn chồn bước đi
Áo chàm đưa buổi phân ly
Cầm tay nhau biết nói gì hôm nay...
(Việt Bắc – Tố Hữu)
Biện pháp tu từ nào được sử dụng trong câu thơ “Áo chàm đưa buổi phân li”?
Đọc đoạn trích sau và trả lời câu hỏi:
Tiếng ai tha thiết bên cồn
Bâng khuâng trong dạ, bồn chồn bước đi
Áo chàm đưa buổi phân ly
Cầm tay nhau biết nói gì hôm nay...
(Việt Bắc – Tố Hữu)
Biện pháp tu từ nào được sử dụng trong câu thơ “Áo chàm đưa buổi phân li”?
Xem đáp án »
06/08/2024
1,911
Câu 5:
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thời gian chạy qua tóc mẹ
Một màu trắng đến nôn nao
Lưng mẹ cứ còng dần xuống
Cho con ngày một thêm cao.
(Trong lời mẹ hát – Trương Nam Hương)
Biện pháp nghệ thuật nào được sử dụng trong câu thơ: “Thời gian chạy qua tóc mẹ”?
Đọc đoạn trích sau đây và trả lời câu hỏi:
Thời gian chạy qua tóc mẹ
Một màu trắng đến nôn nao
Lưng mẹ cứ còng dần xuống
Cho con ngày một thêm cao.
(Trong lời mẹ hát – Trương Nam Hương)
Biện pháp nghệ thuật nào được sử dụng trong câu thơ: “Thời gian chạy qua tóc mẹ”?
Xem đáp án »
06/08/2024
1,841
Câu 6:
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2021\,;\,\,2021} \right]\) để đồ thị hàm số \(y = \frac{{x + 2}}{{\sqrt {{x^2} - 2x + m} }}\) có hai đường tiệm cận đứng?
Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 2021\,;\,\,2021} \right]\) để đồ thị hàm số \(y = \frac{{x + 2}}{{\sqrt {{x^2} - 2x + m} }}\) có hai đường tiệm cận đứng?
Xem đáp án »
19/06/2024
1,651
Câu 7:
Nguyên nhân chủ yếu tạo nên sự khác biệt về trình độ phát triển kinh tế-xã hội giữa nhóm nước phát triển với đang phát triển là
Xem đáp án »
06/08/2024
1,529
🔥 Đề thi HOT:
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 2)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 13)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận