Dung dịch X chứa \(0,02\;{\rm{mol}}\,{\rm{A}}{{\rm{l}}^{3 + }};0,04\;{\rm{mol}}\,{\rm{M}}{{\rm{g}}^{2 + }};0,04\;{\rm{mol}}\,{\rm{NO}}_3^ - ;\,x\,{\rm{mol}}\,{\rm{C}}{{\rm{l}}^ - }\)và y mol \(C{u^{2 + }}.\) Cho X tác dụng hết với dung dịch \({\rm{AgN}}{{\rm{O}}_3}\)dư, thu được 17,22 gam kết tủa. Mặt khác, cho \(170{\rm{ml}}\) dung dịch \({\rm{NaOH}}\)\(1{\rm{M}}\) vào X, thu được \({\rm{m}}\) gam kết tủa. Biết các phản ứng đều xảy ra hoàn toàn. Giá trị của m là
Quảng cáo
Trả lời:
Dung dịch X tác dụng hết dung dịch \(AgN{O_3}\)dư, thu được 17,22 gam kết tủa AgCl.
Þ \({n_{AgCl}} = \frac{{17,22}}{{143,5}} = 0,12\,mol \Rightarrow {n_{C{l^ - }\,(X)}} = 0,12\,mol\)
Xét trong dung dịch X ta có:
+ Bảo toàn điện tích \( \Rightarrow {{\rm{n}}_{{\rm{C}}{{\rm{u}}^{2 + }}}} = 0,01\;{\rm{mol}}.\)
+ Cho dung dịch \(X + 0,17\;{\rm{mol}}\,{\rm{NaOH}}.\)
Mà để tạo \(0,04\;{\rm{mol}}\,\,{\rm{Mg}}{({\rm{OH}})_2}\)và \(0,01\;{\rm{mol}}\,{\rm{Cu}}{({\rm{OH}})_2}\) tốn \(0,1\;{\rm{mol}}\,{\rm{NaOH}}.\)
Þ Còn 0,07 mol NaOH tác dụng với \({\rm{A}}{{\rm{l}}^{3 + }}.\)
\( \Rightarrow {{\rm{n}}_{{\rm{Al}}{{({\rm{OH}})}_3} \downarrow }} = 4{n_{A{l^{3 + }}}} - {n_{{\rm{O}}{{\rm{H}}^ - }}} = 4 \cdot 0,02 - 0,07 = 0,01\;{\rm{mol}}.\)
\( \Rightarrow {m_ \downarrow } = {m_{Mg{{(OH)}_2}}} + {m_{Cu{{(OH)}_2}}} + {m_{Al{{(OH)}_3}}} = 0,04 \cdot 58 + 0,01 \cdot 98 + 0,01 \cdot 78 = 4,08\) gam. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
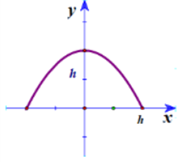
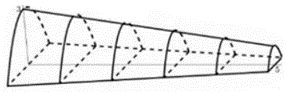
Xét trên một thiết diện parabol có chiều cao là \(h\) và độ dài đáy là \[2h\] và chọn hệ trục \[Oxy\] như hình vẽ.
Parabol \(\left( P \right)\) có phương trình \(\left( P \right):y = a{x^2} + h\,\,(a < 0)\)
Có \[B\left( {h\,;\,\,0} \right) \in (P) \Leftrightarrow 0 = a{h^2} + h \Leftrightarrow a = - \frac{1}{h}\] (do \(h > 0)\)Diện tích \(S\) của thiết diện là: \(S = \int\limits_{ - h}^h {\left( { - \frac{1}{h}{x^2} + h} \right)} \,dx = \frac{{4{h^2}}}{3},\,\,h = 3 - \frac{2}{5}x\)\( \Rightarrow S\left( x \right) = \frac{4}{3}{\left( {3 - \frac{2}{5}x} \right)^2}.\)
Suy ra thể tích không gian bên trong của đường hầm mô hình:
\(V = \int\limits_0^5 {S\left( x \right)} \,dx = \int\limits_0^5 {\frac{4}{3}} {\left( {3 - \frac{2}{5}x} \right)^2}dx \approx 28,888\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)\( \Rightarrow V \approx 29\,\,{\rm{c}}{{\rm{m}}^3}.\)
Câu 2
Lời giải
Gọi chiều rộng của mặt đáy của bể cá là \(a\,\,(m),\,\,a > 0.\)
\( \Rightarrow \) chiều dài của mặt đáy bể cá là \(2a\,\,(\;{\rm{m}}).\)
Gọi chiều cao bể cá là \(h\,\,(m).\)
Diện tích xung quanh của bể cá là \[{S_{xq}} = 2h\left( {a + 2a} \right) = 6ah\,\,\left( {{m^2}} \right).\]
Diện tích đáy của bể cá là \({S_d} = 2{a^2}\,\,\left( {\;{{\rm{m}}^2}} \right).\)
Ông Bình sử dụng hết \(5,5\;\,{{\rm{m}}^2}\) kính để làm một bể cá không nắp nên ta có
\(6ah + 2{a^2} = 5,5 \Rightarrow h = \frac{{5,5 - 2{a^2}}}{{6a}}\,\,(m).\)
Dung tích bể cá là \(V = a \cdot 2a \cdot \frac{{5,5 - 2{a^2}}}{{6a}} = \frac{{\left( {5,5 - 2{a^2}} \right)a}}{3}\,\,\left( {\;{{\rm{m}}^3}} \right).\)
Xét hàm số \[f\left( a \right) = \left( {5,5 - 2{a^2}} \right)a = 5,5a - 2{a^3}.\]
Có \[f'\left( a \right) = 5,5 - 6{a^2}\,;\,\,f' = 0 \Leftrightarrow 5,5 - 6{a^2} = 0 \Rightarrow a = \frac{{\sqrt {33} }}{6}.\]
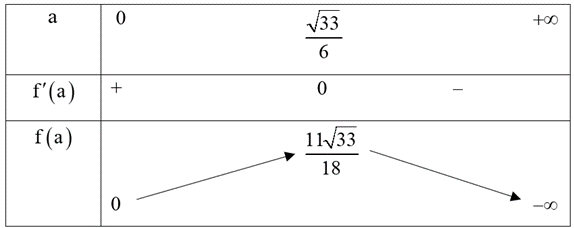
Ta có bảng biến thiên
Vậy \(maxV = \frac{1}{3}f(a) = \frac{1}{3} \cdot \frac{{11\sqrt {33} }}{{18}} \approx 1,17\,\;\left( {{{\rm{m}}^3}} \right).\) Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.