Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 5)
75 người thi tuần này 4.6 2.7 K lượt thi 150 câu hỏi 150 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 45)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 44)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 43)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 42)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 41)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 40)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 39)
Bộ 45 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 38)
Danh sách câu hỏi:
Câu 1
Lời giải
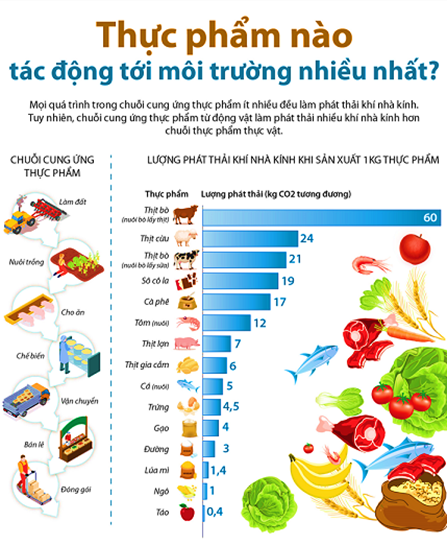
Thực phẩm tác động tới môi trường nhiều nhất là thịt bò. Chọn D.
Câu 2
Lời giải
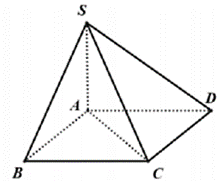
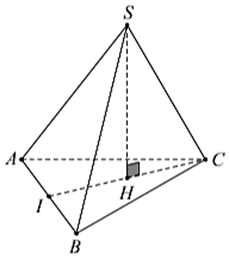
Vì hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với đáy.
Mà \(\left( {SAB} \right) \cap \left( {SAD} \right) = SA\) nên \(SA \bot \left( {ABCD} \right).\)
Ta có: \(AC = a\sqrt 2 \,;\,\,SA = \sqrt {S{C^2} - A{C^2}} = \sqrt {{{\left( {a\sqrt 3 } \right)}^2} - {{\left( {a\sqrt 2 } \right)}^2}} = a.\)Thể tích khối chóp S.ABCD là: \({V_{S \cdot ABCD}} = \frac{1}{3}SA \cdot {S_{ABCD}} = \frac{1}{3}a \cdot {a^2} = \frac{{{a^3}}}{3}.\) Chọn B.
Câu 3
Lời giải
Số tiền bỏ heo của An mỗi ngày tạo thành một cấp số cộng có số hạng đầu \({u_1} = 1000\), công sai \(d = 1000.{\rm{ }}\)
Tổng số tiền bỏ heo tính đến ngày thứ \(n\) là: \({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2} = \frac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2}\).
Tính đến ngày 30 tháng 4 năm 2018 (tính đến ngày thứ 89) tổng số tiền bỏ heo là:
\({S_{89}} = \frac{{89\left[ {2 \cdot 1000 + \left( {89 - 1} \right) \cdot 1000} \right]}}{2} = 4\,\,005\,\,000\) (đồng). Chọn C.
Câu 4
Lời giải
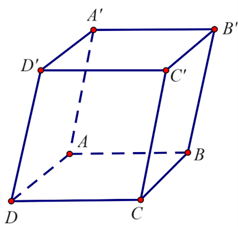
Gọi \(C'\left( {x\,;\,\,y\,;\,\,z} \right).\)
Ta có \(\overrightarrow {AB} = \left( {3\,;\,\,2\,;\,\,0} \right),\,\,\overrightarrow {AD} = \left( {3\,;\,\,0\,;\,\,1} \right),\,\,\overrightarrow {AA'} = \left( {4\,;\,\,2\,;\,\,3} \right).\)
Mà \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \Rightarrow \overrightarrow {AC'} = \left( {10\,;\,\,4\,;\,\,4} \right)\)
\[ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 10 + 3}\\{y = 4 - 0}\\{z = 4 - 0}\end{array} \Rightarrow C'\left( {13\,;\,\,4\,;\,\,4} \right).} \right.\] Chọn C.Câu 5
Lời giải
Sử dụng MTCT ta có phương trình \({z^3} - 6{z^2} + 12z - 7 = 0\) có 3 nghiệm \({z_1} = 1\,;\,\,{z_2} = \frac{5}{2} + \frac{{\sqrt 3 }}{2}i\,;\,\,{z_3} = \frac{5}{2} - \frac{{\sqrt 3 }}{2}i.\) Suy ra: \[A\left( {1\,;\,\,0} \right),\,\,B\left( {\frac{5}{2}\,;\,\,\frac{{\sqrt 3 }}{2}} \right),\,\,C\left( {\frac{5}{2}\,;\,\, - \frac{{\sqrt 3 }}{2}} \right).\]
\(AB = \left| {\overrightarrow {AB} } \right| = \sqrt {\frac{9}{4} + \frac{3}{4}} = \sqrt 3 {\rm{; }}\)\[AC = \left| {\overrightarrow {AC} } \right| = \sqrt {\frac{9}{4} + \frac{3}{4}} = \sqrt 3 \,;\,\,BC = \left| {\overrightarrow {BC} } \right| = \sqrt 3 .\]
\( \Rightarrow \Delta ABC\) đều cạnh \(\sqrt 3 .\) Vậy \({S_{ABC}} = \frac{{{{\left( {\sqrt 3 } \right)}^2}\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{4}.\) Chọn D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(T = 12.\)
B. \(T = - 7.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 14
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. 20 xe loại chở 3 tấn, 19 xe loại chở 5 tấn và 18 xe loại chở \[7,5\] tấn.
B. 18 xe loại chở 3 tấn, 19 xe loại chở 5 tấn và 20 xe loại chở \[7,5\] tấn.
C. 19 xe loại chở 3 tấn, 20 xe loại chở 5 tấn và 18 xe loại chở \[7,5\] tấn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. 4036
B. 4037
C. 2018
D. 2019
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. \(I = 4.\)
B. \(I = 5.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. \(2x - 2y + z + 2 = 0.\)
B. \(2x - 2y + z - 16 = 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A. \(\frac{{a\sqrt {21} }}{{14}}.\)
B. \(\frac{{a\sqrt {14} }}{8}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 51
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 52
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 53
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 54
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 55
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 56
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 57
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 58
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 59
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 60
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 62
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 63
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 64
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 65
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 66
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 67
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 68
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 69
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 70
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 71
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 72
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 73
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 74
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 75
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 76
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 77
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 78
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 79
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 80
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 81
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 82
A. làm thất bại chiến tranh xâm lược của Mĩ.
B. Buộc thực dân Pháp phải phân tán lực lượng.
C. đánh bại chiến tranh tổng lực của Mĩ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 83
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 84
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 85
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 86
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 87
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 88
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 89
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 90
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 92
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 93
C. ven biển Nam Trung Bộ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 94
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 95
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 96
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 97
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 98
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 99
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 100
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 101
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 102
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 103
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 104
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 105
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 106
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 107
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 108
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 109
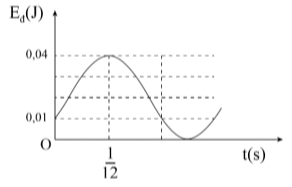
A. \(10\;{\rm{cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
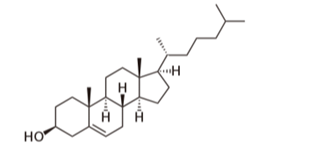
Câu 111
A. \({{\rm{C}}_{27}}{{\rm{H}}_{46}}{\rm{O}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 112
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 114
A. \({{\rm{H}}_2}{\rm{NC}}{{\rm{H}}_2}{\rm{COOH}}\) và \({{\rm{H}}_2}{\rm{N}}{{\rm{C}}_4}{{\rm{H}}_8}{\rm{COOH}}.\)
B. \({{\rm{H}}_2}{\rm{NC}}{{\rm{H}}_2}{\rm{COOH}}\) và \({{\rm{H}}_2}{\rm{N}}{{\rm{C}}_3}{{\rm{H}}_6}{\rm{COOH}}.\)
C. \({{\rm{H}}_2}{\rm{N}}{{\rm{C}}_2}{{\rm{H}}_4}{\rm{COOH}}\) và \({{\rm{H}}_2}{\rm{N}}{{\rm{C}}_3}{{\rm{H}}_6}{\rm{COOH}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 116
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 118
A. \({\rm{N}}{{\rm{H}}_4}{\rm{Cl}},{\rm{N}}{{\rm{H}}_3},{\rm{C}}{{\rm{H}}_3}{\rm{COOH}},{\rm{HCl}},{\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3}.\)
B. \({\rm{C}}{{\rm{H}}_3}{\rm{COOH}},{\rm{N}}{{\rm{H}}_3},{\rm{N}}{{\rm{H}}_4}{\rm{Cl}},{\rm{HCl}},{\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3}.\)
C. \({\rm{N}}{{\rm{H}}_4}{\rm{Cl}},{\rm{N}}{{\rm{a}}_2}{\rm{C}}{{\rm{O}}_3},{\rm{C}}{{\rm{H}}_3}{\rm{COOH}},{\rm{HCl}},{\rm{N}}{{\rm{H}}_3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 119
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 121
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 122
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 123
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 124
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 126
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 127
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 128
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 129
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 1
Đọc đoạn trích sau và trả lời các câu hỏi từ 51 đến 55:
Tiếng trống thu không trên cái chòi của huyện nhỏ; từng tiếng một vang ra để gọi buổi chiều. Phương tây đỏ rực như lửa cháy và những đám mây ánh hồng như hòn than sắp tàn. Dãy tre làng trước mặt đen lại và cắt hình rõ rệt trên nền trời.
Chiều, chiều rồi. Một chiều êm ả như ru, văng vẳng tiếng ếch nhái kêu ran ngoài đồng ruộng theo gió nhẹ đưa vào. Trong cửa hàng hơi tối muỗi đã bắt đầu vo ve. Liên ngồi yên lặng bên mấy quả thuốc sơn đen; đôi mắt chị bóng tối ngập đầy dần và cái buồn của buổi chiều quê thấm thía vào tâm hồn ngây thơ của chị; Liên không hiểu sao, nhưng chị thấy lòng buồn man mác trước cái giờ khắc của ngày tàn.
(Hai đứa trẻ – Thạch Lam)
Câu 131
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 132
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 133
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 134
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 135
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 2
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 56 đến 60:
Cơ quan cảm giác của động vật và của con người bao gồm 5 loại: thị giác, thính giác, khứu giác, vị giác và xúc giác. Chúng là cửa sổ cảm nhận sự vật hiện tượng thế giới bên ngoài của động vật và con người. Loài cá cũng có một cơ quan cảm giác đặc biệt. Đó là: trắc tuyến (tuyến gồm nhiều chấm nhỏ ở hai bên cơ thể cá, chứa các tế bào cảm giác nhận biết phương hướng và áp lực của dòng nước).
Nếu bạn chú ý quan sát con cá sẽ phát hiện một lớp vẩy ở giữa 2 mặt bên, mỗi bên có một tuyến được tạo thành bởi nhiều lỗ nhỏ đó là trắc tuyến, chỉ có điều là số lượng trắc tuyến và sự phân bố của chúng khác nhau.
Thực ra, trắc tuyến của loài cá là một cái ống nhỏ bé, ẩn trong lớp da theo sự giãn cách nhất định, thông qua lớp vẩy để thông ra bên ngoài, nhìn nó trông giống như hư tuyến. Trắc tuyến tự liên kết với thần kinh, mỗi khi có dòng nước chảy với cường độ lớn qua thân thể của con cá, dòng nước đó sẽ làm cho trắc tuyến của con cá sản sinh ra các hooc-môn tương ứng. Từ đó tạo ra phản ứng chạy trốn, né tránh. Các loài cá đã dựa vào trắc tuyến để xác định phương hướng, cảm nhận dòng nước.
Dựa trên trắc tuyến cá có thể cảm nhận được mối nguy hiểm của dòng nước, từ đó chúng kịp thời thay đổi phương hướng, vượt qua một cách an toàn. Ngoài ra chúng còn có thể cảm nhận được sự bơi nhảy của những sinh vật nổi trên mặt nước như những con tôm, cá nhỏ. Từ đó có thể bắt chúng một cách chính xác. Khi loài cá bơi lội thành từng đàn, chúng có thể thông qua trắc tuyến để duy trì sự liên lạc với đồng loại tránh bị thất lạc hoặc mất phương hướng. Trong cuộc sống của những loài cá có thị giác không phát triển thậm chí hoàn toàn không có thị giác, vai trò của trắc tuyến càng có ý nghĩa rất quan trọng đối với chúng. Cá không thể nào nhìn được tất cả những sự vật xung quanh chúng, chúng hoàn toàn dựa vào sự nhận biết của trắc tuyến. Nếu không có trắc tuyến các loài cá sẽ không có cách nào để duy trì cuộc sống của chúng ở biển khơi mênh mông hoặc trong các ao, hồ, sông, suối.
(Phương Hiếu, Bí mật về thế giới động vật, NXB Lao động, 2015, tr.64)
Câu 136
D. Trắc tuyến của loài cá là một cái ống nhỏ bé, ẩn trong lớp da theo sự giãn cách nhất định.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 137
A. Duy trì sự liên lạc với đồng loại tránh bị thất lạc hoặc mất phương hướng.
B. Cảm nhận được mối nguy hiểm của dòng nước.
C. Nhìn được tất cả những sự vật xung quanh chúng.
D. Giúp cá bơi nhanh hơn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 138
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 139
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 140
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 3
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 61 đến 65:
Bản lĩnh là khi bạn dám nghĩ, dám làm và có thái độ sống tốt. Muốn có bản lĩnh bạn cũng phải kiên trì luyện tập. Chúng ta thường yêu thích những người có bản lĩnh sống. Bản lĩnh đúng nghĩa chỉ có được khi bạn biết đặt ra mục tiêu và phương pháp để đạt được mục tiêu đó. Nếu không có phương pháp thì cũng giống như bạn đang nhắm mắt chạy trên con đường có nhiều ổ gà. Cách thức ở đây cũng rất đơn giản. Đầu tiên, bạn phải xác định được hoàn cảnh và môi trường để bản lĩnh được thể hiện đúng lúc, đúng nơi, không tùy tiện. Thứ hai bạn phải chuẩn bị cho mình những tài sản bổ trợ như sự tự tin, ý chí, nghị lực, quyết tâm.... Điều thứ ba vô cùng quan trọng chính là khả năng của bạn. Đó là những kĩ năng đã được trau dồi cùng với vốn tri thức, trải nghiệm. Một người mạnh hay yếu quan trọng là tùy thuộc vào yếu tố này. Bản lĩnh tốt là vừa phục vụ được mục đích cá nhân vừa có được sự hài lòng từ những người xung quanh. Khi xây dựng được bản lĩnh, bạn không chỉ thể hiện được bản thân mình mà còn được nhiều người, thừa nhận và yêu mến hơn.
(Xây dựng bản lĩnh cá nhân – Tuoitre.vn)
Câu 141
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 142
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 143
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 144
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 145
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đoạn văn 4
Đọc đoạn trích sau đây và trả lời các câu hỏi từ 66 đến 70:
Khi ta lớn lên Đất Nước đã có rồi
Đất Nước có trong những cái “ngày xửa ngày xưa...” mẹ thường hay kể
Đất Nước bắt đầu với miếng trầu bây giờ bà ăn
Đất Nước lớn lên khi dân mình biết trồng tre mà đánh giặc
Tóc mẹ thì bới sau đầu
Cha mẹ thương nhau bằng gừng cay muối mặn
Cái kèo, cái cột thành tên
Hạt gạo phải một nắng hai sương xay, giã, giần, sàng
Đất Nước có từ ngày đó...
(Trích đoạn trích Đất Nước – Nguyễn Khoa Điềm)
Câu 146
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 147
Câu thơ “Đất Nước lớn lên khi dân mình biết trồng tre mà đánh giặc” gợi nhớ đến truyện dân gian nào?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 148
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 149
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 150
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.