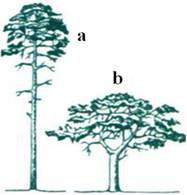
Quan sát hình bên và hãy xác định cây nào (a hoặc b) mọc trong rừng với mật độ cây dày đặc, cây nào mọc nơi trống trải? Cho biết cây a và cây b là cùng một loài.

Quảng cáo
Trả lời:
Nơi sống của cây a có mật độ cây cao nên có thân cao thẳng, cành chỉ tập trung ở phần ngọn để nhận được ánh sáng. Cây b mọc ở nơi trống trải nên có nhiều cành và tán cây rộng để nhận được nhiều ánh sáng. Chọn A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
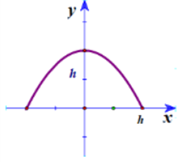
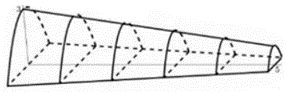
Xét trên một thiết diện parabol có chiều cao là \(h\) và độ dài đáy là \[2h\] và chọn hệ trục \[Oxy\] như hình vẽ.
Parabol \(\left( P \right)\) có phương trình \(\left( P \right):y = a{x^2} + h\,\,(a < 0)\)
Có \[B\left( {h\,;\,\,0} \right) \in (P) \Leftrightarrow 0 = a{h^2} + h \Leftrightarrow a = - \frac{1}{h}\] (do \(h > 0)\)Diện tích \(S\) của thiết diện là: \(S = \int\limits_{ - h}^h {\left( { - \frac{1}{h}{x^2} + h} \right)} \,dx = \frac{{4{h^2}}}{3},\,\,h = 3 - \frac{2}{5}x\)\( \Rightarrow S\left( x \right) = \frac{4}{3}{\left( {3 - \frac{2}{5}x} \right)^2}.\)
Suy ra thể tích không gian bên trong của đường hầm mô hình:
\(V = \int\limits_0^5 {S\left( x \right)} \,dx = \int\limits_0^5 {\frac{4}{3}} {\left( {3 - \frac{2}{5}x} \right)^2}dx \approx 28,888\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\)\( \Rightarrow V \approx 29\,\,{\rm{c}}{{\rm{m}}^3}.\)
Câu 2
Lời giải
Gọi chiều rộng của mặt đáy của bể cá là \(a\,\,(m),\,\,a > 0.\)
\( \Rightarrow \) chiều dài của mặt đáy bể cá là \(2a\,\,(\;{\rm{m}}).\)
Gọi chiều cao bể cá là \(h\,\,(m).\)
Diện tích xung quanh của bể cá là \[{S_{xq}} = 2h\left( {a + 2a} \right) = 6ah\,\,\left( {{m^2}} \right).\]
Diện tích đáy của bể cá là \({S_d} = 2{a^2}\,\,\left( {\;{{\rm{m}}^2}} \right).\)
Ông Bình sử dụng hết \(5,5\;\,{{\rm{m}}^2}\) kính để làm một bể cá không nắp nên ta có
\(6ah + 2{a^2} = 5,5 \Rightarrow h = \frac{{5,5 - 2{a^2}}}{{6a}}\,\,(m).\)
Dung tích bể cá là \(V = a \cdot 2a \cdot \frac{{5,5 - 2{a^2}}}{{6a}} = \frac{{\left( {5,5 - 2{a^2}} \right)a}}{3}\,\,\left( {\;{{\rm{m}}^3}} \right).\)
Xét hàm số \[f\left( a \right) = \left( {5,5 - 2{a^2}} \right)a = 5,5a - 2{a^3}.\]
Có \[f'\left( a \right) = 5,5 - 6{a^2}\,;\,\,f' = 0 \Leftrightarrow 5,5 - 6{a^2} = 0 \Rightarrow a = \frac{{\sqrt {33} }}{6}.\]
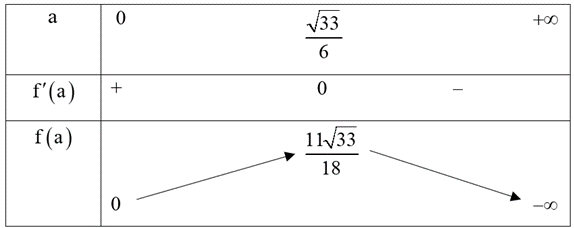
Ta có bảng biến thiên
Vậy \(maxV = \frac{1}{3}f(a) = \frac{1}{3} \cdot \frac{{11\sqrt {33} }}{{18}} \approx 1,17\,\;\left( {{{\rm{m}}^3}} \right).\) Chọn B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.