Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1). Phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính diện tích tứ giác A’B’C’D’.
Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1). Phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính diện tích tứ giác A’B’C’D’.
Câu hỏi trong đề: Giải SBT Toán 9 Bài 2. Phép quay có đáp án !!
Quảng cáo
Trả lời:
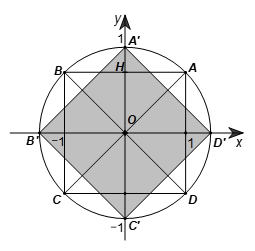
Gọi H là hình chiếu của A trên Oy.
Ta có A(1; 1) nên suy ra AH = OH = 1.
Do đó ∆OAH vuông cân tại H nên \(\widehat {AOH} = 45^\circ .\)
Xét ∆OAH vuông tại H, ta có: OA2 = OH2 + AH2 (định lí Pythagore)
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 .\)
Tương tự, ta sẽ có \(OA = OB = OC = OD = \sqrt 2 .\)
Mặt khác, do ABCD là hình vuông nên hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường, do đó O là tâm của hình vuông.
Do đó, phép quay ngược chiều 45° tâm O biến điểm A thành các điểm A’ nằm trên tia Oy sao cho \(OA' = OA = \sqrt 2 ,\) tức là \[A'\left( {0;\sqrt 2 } \right).\]
Tương tự, ta chứng minh được, phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm \[A'\left( {0;\sqrt 2 } \right),\,\,B'\left( { - \sqrt 2 ;0} \right),\] \(C'\left( {0; - \sqrt 2 } \right),\,\,D'\left( {\sqrt 2 ;0} \right).\)
Suy ra tứ giác A’B’C’D’ là hình vuông với hai đường chéo là A’C’ và B’D’, nên diện tích tứ giác A’B’C’D’ là:
\(\frac{1}{2} \cdot A'C' \cdot B'D' = \frac{1}{2} \cdot 2\sqrt 2 \cdot 2\sqrt 2 = 4\) (đơn vị diện tích).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
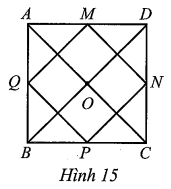
a) Xét ∆ABC có Q, P lần lượt là trung điểm của AB, BC nên QP là đường trung bình của tam giác, do đó QP // AC và \(QP = \frac{1}{2}AC.\)
Tương tự, ta có: MN là đường trung bình của tam giác ACD, do đó MN // AC và \(MN = \frac{1}{2}AC.\)
Do đó MNPQ là hình bình hành.
Mặt khác, ta cũng chứng minh được MQ là đường trung bình của ∆ABD nên \(MQ = \frac{1}{2}BD.\)
Lại có ABCD là hình vuông nên AC = BD và AC ⊥ BD.
Suy ra MN = MQ và MN ⊥ MQ.
Khi đó hình bình hành MNPQ là hình vuông.
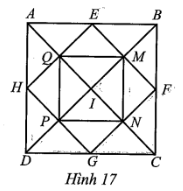
b) ⦁ Phép quay ngược chiều 90° tâm O biến điểm O tương ứng thành chính nó.
⦁ Do ABCD là hình vuông tâm O nên OA = OB = OC = OD.
Theo câu a, ta có \(\widehat {AOD} = 90^\circ \)
Do đó, tia OD quay ngược chiều 90° tâm O đến tia OA.
⦁ Tương tự, đối với hình vuông MNPQ ta cũng có ON = OM và \(\widehat {NOM} = 90^\circ \) nên tia ON quay ngược chiều 90° tâm O đến tia OM.
Vậy phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm O, A, M.
c) Các phép quay tâm O giữ nguyên hình vuông MNPQ là các phép quay thuận chiều α° tâm O và các phép quay ngược chiều α° tâm O, với α° lần lượt nhận các giá trị:
α1° = 90°; α2° = 180°; α3° = 270°; α4° = 360°.
Lời giải
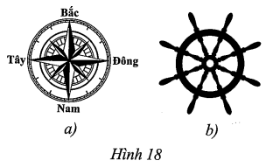
a) Do con thuyền đang đi về hướng Bắc, nên để con tàu rẽ sang hướng Tây thì bánh lái cần quay sang trái (quay ngược chiều kim đồng hồ) một góc 90°.
Vậy bác An cần thực hiện phép quay ngược chiều 90° tâm là tâm của bánh lái.
b) Do con thuyền đang đi về hướng Bắc, nên để con tàu rẽ sang hướng Đông thì bánh lái cần quay sang phải (quay thuận chiều kim đồng hồ) một góc 90°.
Vậy bác An cần thực hiện phép quay thuận chiều 90° tâm là tâm của bánh lái.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.