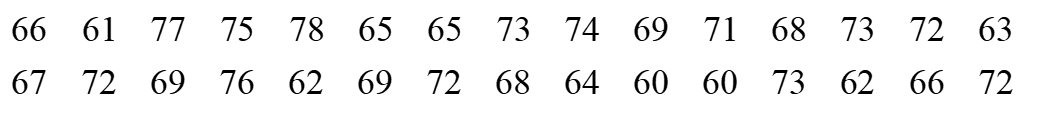Câu hỏi:
28/08/2024 1,651
Một nhà máy tổ chức thi tuyển kĩ thuật viên mới. Thời gian hoàn thành một bài thực hành của các ứng viên được ghi lại ở bảng sau (đơn vị: giây).
a) Hãy chia số liệu trên thành 5 nhóm với nhóm đầu tiên là [300; 350). Tìm tần số và tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu ghép nhóm đó.
c) Người ta sẽ loại 40% ứng viên có thời gian hoàn thành bài thi lâu nhất. Hỏi các thí sinh có thời gian hoàn thành bài thi trên bao nhiêu giây sẽ bị loại?
Một nhà máy tổ chức thi tuyển kĩ thuật viên mới. Thời gian hoàn thành một bài thực hành của các ứng viên được ghi lại ở bảng sau (đơn vị: giây).
a) Hãy chia số liệu trên thành 5 nhóm với nhóm đầu tiên là [300; 350). Tìm tần số và tần số tương đối của mỗi nhóm đó.
b) Lập bảng tần số ghép nhóm và bảng tần số tương đối ghép nhóm cho mẫu số liệu ghép nhóm đó.
c) Người ta sẽ loại 40% ứng viên có thời gian hoàn thành bài thi lâu nhất. Hỏi các thí sinh có thời gian hoàn thành bài thi trên bao nhiêu giây sẽ bị loại?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Cỡ mẫu N = 30.
Các nhóm số liệu lần lượt là [300; 350); [350; 400); [400; 450); [450; 500); [500; 550).
Tần số tương đối của 5 nhóm trên lần lượt là m1 = 4; m2 = 6; m3 = 8; m4 = 9; m5 = 3. Gọi f1, f2, f3, f4, f5 lần lượt là tần số tương đối của các nhóm số liệu trên.
Ta có:
\({f_1} = \frac{4}{{30}} \cdot 100\% \approx 13,3\% ;\,\,\,{f_2} = \frac{6}{{30}} \cdot 100\% = 20\% ;\,\,\,{f_3} = \frac{8}{{30}} \cdot 100\% \approx 26,7\% ;\)
\({f_4} = \frac{9}{{30}} \cdot 100\% = 30\% ;\,\,\,{f_5} = \frac{3}{{30}} \cdot 100\% = 10\% .\)
b) Bảng tần số ghép nhóm:
|
Thời gian (giây) |
[300; 350) |
[350; 400) |
[400; 450) |
[450; 500) |
[500; 550) |
|
Tần số |
4 |
6 |
8 |
9 |
3 |
Bảng tần số tương đối ghép nhóm:
|
Thời gian (giây) |
[300; 350) |
[350; 400) |
[400; 450) |
[450; 500) |
[500; 550) |
|
Tần số tương đối |
13,3% |
20,0% |
26,7% |
30,0% |
10,0% |
c) Tần số tương đối của các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên là: 30% + 10% = 40%.
Vậy các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên sẽ bị loại.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Gọi f1, f2, f3, f4, f5 lần lượt là tần số tương đối của các nhóm [8; 9); [9; 10); [10; 11); [11; 12); [12; 13).
Ta có:
\({f_1} = \frac{{18}}{{40}} \cdot 100\% = 45\% ;\) \({f_2} = \frac{{10}}{{40}} \cdot 100\% = 25\% ;\) \({f_3} = \frac{6}{{40}} \cdot 100\% = 15\% ;\)
\({f_4} = \frac{4}{{40}} \cdot 100\% = 10\% ;\) \({f_5} = \frac{2}{{40}} \cdot 100\% = 5\% .\)
b) Bảng tần số tương đối ghép nhóm:
|
Độ dài (m) |
[8; 9) |
[9; 10) |
[10; 11) |
[11; 12) |
[12; 13) |
|
Tần số tương đối |
45% |
25% |
15% |
10% |
5% |
c) Giá trị đại điện của các nhóm [8; 9); [9; 10); [10; 11); [11; 12); [12; 13) lần lượt là 8,5; 9,5; 10,5; 11,5; 12,5.
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
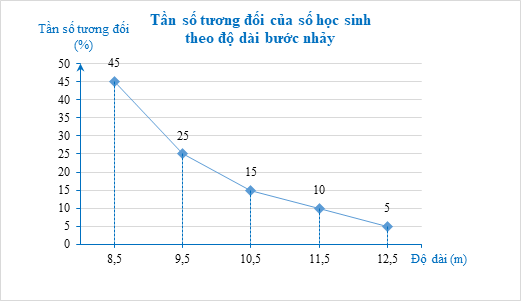
d) Hai nhóm [11; 12) và [12; 13) có tổng tần số tương đối là 10% + 5% = 15%.
Do đó, giáo viên nên chọn các học sinh có thành tích nhảy 3 bước tối thiểu là 11 m.
Lời giải
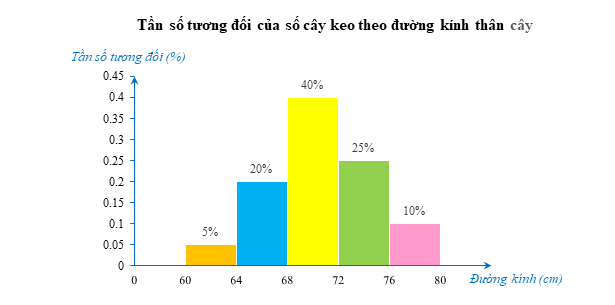
a) Gọi m1, m2, m3, m4, m5 lần lượt là tần số của các nhóm [60; 64); [64; 68); [68; 72); [72; 76); [76; 80).
Ta có: m1 = 80.5% = 4; m2 = 80.20% = 16;
m3 = 80.40% = 32; m4 = 80.25% = 20; m5 = 80.10% = 8.
Bảng tần số ghép nhóm của mẫu số liệu:
|
Đường kính (cm) |
[60; 64) |
[64; 68) |
[68; 72) |
[72; 76) |
[76; 80) |
|
Tần số |
4 |
16 |
32 |
20 |
8 |
b) Tần số tương đối của số cây keo có đường kính thân cây từ 72 cm trở lên là \[25\% + 10\% = 35\% > \frac{1}{3}.\]
Vậy ý kiến cho rằng \(\frac{1}{3}\) số cây của keo có đường kính thân cây từ 72 cm trở lên là chính xác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận