Biểu đồ dưới đây biểu diễn mẫu số liệu ghép nhóm về đường kính thân (đơn vị: cm) của 80 cây keo trồng tại một lâm trường.
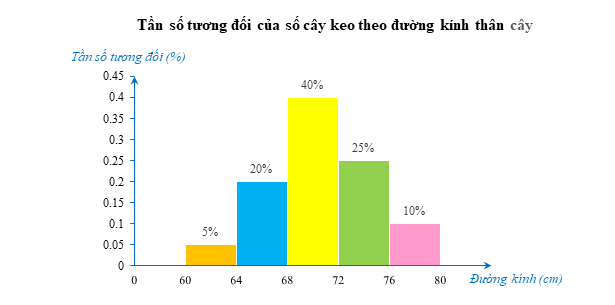
a) Hãy tìm tần số của mỗi nhóm số liệu và lập bảng tần số tương đối ghép nhóm.
b) Có ý kiến cho rằng \(\frac{1}{3}\) số cây của keo có đường kính thân cây từ 72 cm trở lên. Ý kiến trên có chính xác không? Tại sao?
Biểu đồ dưới đây biểu diễn mẫu số liệu ghép nhóm về đường kính thân (đơn vị: cm) của 80 cây keo trồng tại một lâm trường.
a) Hãy tìm tần số của mỗi nhóm số liệu và lập bảng tần số tương đối ghép nhóm.
b) Có ý kiến cho rằng \(\frac{1}{3}\) số cây của keo có đường kính thân cây từ 72 cm trở lên. Ý kiến trên có chính xác không? Tại sao?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Gọi m1, m2, m3, m4, m5 lần lượt là tần số của các nhóm [60; 64); [64; 68); [68; 72); [72; 76); [76; 80).
Ta có: m1 = 80.5% = 4; m2 = 80.20% = 16;
m3 = 80.40% = 32; m4 = 80.25% = 20; m5 = 80.10% = 8.
Bảng tần số ghép nhóm của mẫu số liệu:
|
Đường kính (cm) |
[60; 64) |
[64; 68) |
[68; 72) |
[72; 76) |
[76; 80) |
|
Tần số |
4 |
16 |
32 |
20 |
8 |
b) Tần số tương đối của số cây keo có đường kính thân cây từ 72 cm trở lên là \[25\% + 10\% = 35\% > \frac{1}{3}.\]
Vậy ý kiến cho rằng \(\frac{1}{3}\) số cây của keo có đường kính thân cây từ 72 cm trở lên là chính xác.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Gọi f1, f2, f3, f4, f5 lần lượt là tần số tương đối của các nhóm [8; 9); [9; 10); [10; 11); [11; 12); [12; 13).
Ta có:
\({f_1} = \frac{{18}}{{40}} \cdot 100\% = 45\% ;\) \({f_2} = \frac{{10}}{{40}} \cdot 100\% = 25\% ;\) \({f_3} = \frac{6}{{40}} \cdot 100\% = 15\% ;\)
\({f_4} = \frac{4}{{40}} \cdot 100\% = 10\% ;\) \({f_5} = \frac{2}{{40}} \cdot 100\% = 5\% .\)
b) Bảng tần số tương đối ghép nhóm:
|
Độ dài (m) |
[8; 9) |
[9; 10) |
[10; 11) |
[11; 12) |
[12; 13) |
|
Tần số tương đối |
45% |
25% |
15% |
10% |
5% |
c) Giá trị đại điện của các nhóm [8; 9); [9; 10); [10; 11); [11; 12); [12; 13) lần lượt là 8,5; 9,5; 10,5; 11,5; 12,5.
Biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
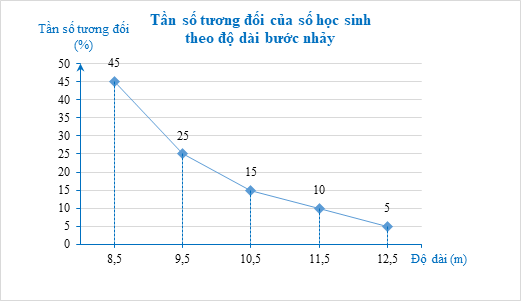
d) Hai nhóm [11; 12) và [12; 13) có tổng tần số tương đối là 10% + 5% = 15%.
Do đó, giáo viên nên chọn các học sinh có thành tích nhảy 3 bước tối thiểu là 11 m.
Lời giải
a) Cỡ mẫu N = 30.
Các nhóm số liệu lần lượt là [300; 350); [350; 400); [400; 450); [450; 500); [500; 550).
Tần số tương đối của 5 nhóm trên lần lượt là m1 = 4; m2 = 6; m3 = 8; m4 = 9; m5 = 3. Gọi f1, f2, f3, f4, f5 lần lượt là tần số tương đối của các nhóm số liệu trên.
Ta có:
\({f_1} = \frac{4}{{30}} \cdot 100\% \approx 13,3\% ;\,\,\,{f_2} = \frac{6}{{30}} \cdot 100\% = 20\% ;\,\,\,{f_3} = \frac{8}{{30}} \cdot 100\% \approx 26,7\% ;\)
\({f_4} = \frac{9}{{30}} \cdot 100\% = 30\% ;\,\,\,{f_5} = \frac{3}{{30}} \cdot 100\% = 10\% .\)
b) Bảng tần số ghép nhóm:
|
Thời gian (giây) |
[300; 350) |
[350; 400) |
[400; 450) |
[450; 500) |
[500; 550) |
|
Tần số |
4 |
6 |
8 |
9 |
3 |
Bảng tần số tương đối ghép nhóm:
|
Thời gian (giây) |
[300; 350) |
[350; 400) |
[400; 450) |
[450; 500) |
[500; 550) |
|
Tần số tương đối |
13,3% |
20,0% |
26,7% |
30,0% |
10,0% |
c) Tần số tương đối của các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên là: 30% + 10% = 40%.
Vậy các ứng viên có thời gian hoàn thành bài thi từ 450 giây trở lên sẽ bị loại.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo