Câu hỏi:
28/08/2024 538
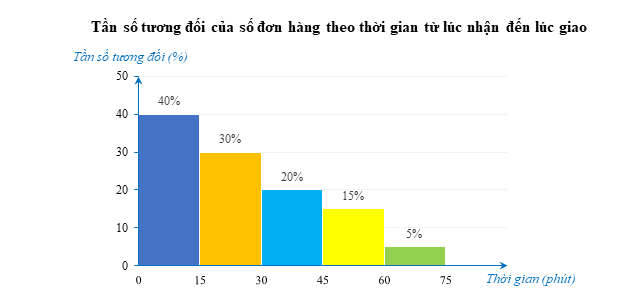
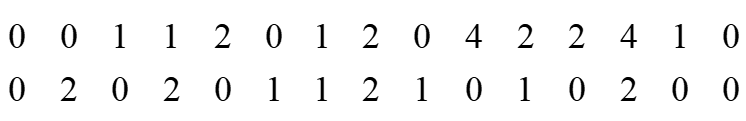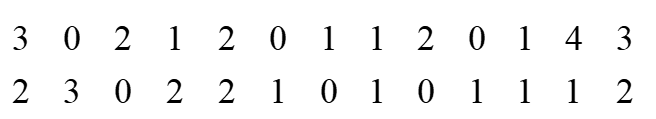Vào đầu năm học, người ta lựa chọn ngẫu nhiên một số học sinh lớp 9 ở khu vực A và khu vực B để kiểm tra tình trạng cân nặng. Kết quả khảo sát được ghi lại ở bảng sau:
Tình trạng cân nặng
Thiếu cân
Bình thường
Thừa cân
Béo phì
Số học sinh khu vực A
16
40
16
8
Số học sinh khu vực B
6
34
5
5
a) Hãy tính tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng.
b) Hãy lựa chọn, vẽ biểu đồ phù hợp và so sánh tình trạng cân nặng của học sinh ở hai khu vực.
Vào đầu năm học, người ta lựa chọn ngẫu nhiên một số học sinh lớp 9 ở khu vực A và khu vực B để kiểm tra tình trạng cân nặng. Kết quả khảo sát được ghi lại ở bảng sau:
|
Tình trạng cân nặng |
Thiếu cân |
Bình thường |
Thừa cân |
Béo phì |
|
Số học sinh khu vực A |
16 |
40 |
16 |
8 |
|
Số học sinh khu vực B |
6 |
34 |
5 |
5 |
a) Hãy tính tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng.
b) Hãy lựa chọn, vẽ biểu đồ phù hợp và so sánh tình trạng cân nặng của học sinh ở hai khu vực.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) * Khu vực A:
Cỡ mẫu N = 16 + 40 + 16 + 8 = 80.
Tần số của các nhóm thiếu cân, bình thường, thừa cân, béo phì lần lượt là m1 = 16; m2 = 40; m3 = 16; m4 = 8.
Gọi f1, f2, f3, f4, f5 lần lượt là tần số tương đối của các nhóm thiếu cân, bình thường, thừa cân, béo phì.
Ta có: \({f_1} = \frac{{16}}{{80}} \cdot 100\% = 20\% ;\) \({f_2} = \frac{{40}}{{80}} \cdot 100\% = 50\% ;\)
\({f_3} = \frac{{16}}{{80}} \cdot 100\% = 20\% ;\) \({f_4} = \frac{8}{{80}} \cdot 100\% = 10\% .\)
* Khu vực B:
Cỡ mẫu N = 6 + 34 + 5 + 5 = 50.
Tần số của các nhóm thiếu cân, bình thường, thừa cân, béo phì lần lượt là m’1 = 6; m’2 = 34; m’3 = 5; m’4 = 5.
Gọi f’1, f’2, f’3, f’4, f’5 lần lượt là tần số tương đối của các nhóm thiếu cân, bình thường, thừa cân, béo phì.
Ta có: \({f'_1} = \frac{6}{{50}} \cdot 100\% = 12\% ;\) \({f'_2} = \frac{{34}}{{50}} \cdot 100\% = 68\% ;\)
\({f'_3} = \frac{5}{{50}} \cdot 100\% = 10\% ;\) \({f'_4} = \frac{5}{{50}} \cdot 100\% = 10\% .\)
Vậy bảng tần số tương đối của học sinh ở mỗi khu vực theo tình trạng cân nặng:
|
Tình trạng cân nặng |
Thiếu cân |
Bình thường |
Thừa cân |
Béo phì |
|
Số học sinh khu vực A |
20% |
50% |
20% |
10% |
|
Số học sinh khu vực B |
12% |
68% |
10% |
10% |
b) Để so sánh tình trạng cân nặng của học sinh ở hai khu vực, ta sử dụng biểu đồ tần số tương đối dạng cột kép.
Biểu đồ cột kép để so sánh tình trạng cân nặng của học sinh ở hai khu vực như sau:
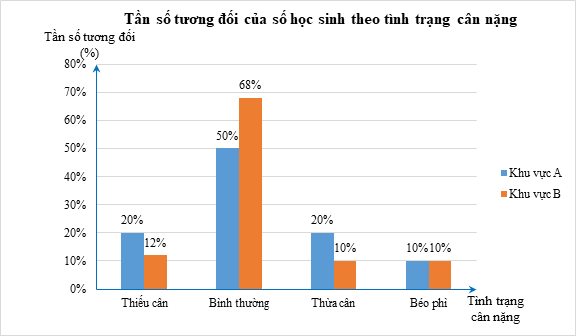
Từ biểu đồ, ta thấy:
⦁ Tần số tương đối của học sinh thiếu cân và thừa cân ở khu vực A cao hơn khu vực B.
⦁ Tần số tương đối của số học sinh có cân nặng bình thường ở khu vực A thấp hơn khu vực B.
⦁ Tần số tương đối của số học sinh béo phì ở hai khu vực là như nhau.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tổng các tần số tương đối là 15% + 25% + 35% + 25% = 100%, nên nếu có số liệu về tần số tương đối sai thì phải có ít nhất hai số liệu sai.
Mà chỉ có một số liệu sai trong bảng nên các giá trị tần số tương đối đều chính xác.
Ta có \(\frac{{10}}{{15}} \ne \frac{{20}}{{25}} = \frac{{28}}{{35}} = \frac{{20}}{{25}}\) do đó số liệu tần số 10 là sai.
Theo tính chất tỉ lệ thức, ta có giá trị đúng là \(\frac{{15 \cdot 20}}{{25}} = 12.\)
Vậy bảng số liệu đúng như sau:
|
Giá trị |
2 |
3 |
4 |
7 |
|
Tần số |
12 |
20 |
28 |
20 |
|
Tần số tương đối |
15% |
25% |
35% |
25% |
Lời giải
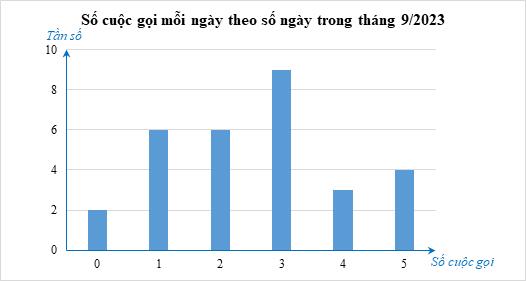
a) Trong các số liệu trên, có 6 giá trị khác nhau là: 0; 1; 2; 3; 4; 5.
Tần số của các giá trị 0; 1; 2; 3; 4; 5 lần lượt là: 2; 6; 6; 9; 3; 4.
b) Bảng tần số:
|
Số cuộc gọi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Tần số |
2 |
6 |
6 |
9 |
3 |
4 |
c) Biểu đồ cột:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
Đề ôn thi vào 10 môn Toán có đáp án (Mới nhất)- Đề số 1