Quảng cáo
Trả lời:
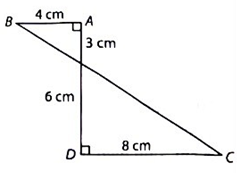
Hình tạo thành là hai hình nón.
Hình nón 1 có: R1 = 4 cm, h1 = 3 cm; hình nón 2 có: R2 = 8 cm, h2 = 6 cm.
Thể tích của hình nón 1 là: \({V_1} = \frac{1}{3}\pi {R_1}^2{h_1} = \frac{1}{3}\pi {.4^2}.3 = 16\pi \) (cm3).
Thể tích của hình nón 2 là: \({V_2} = \frac{1}{3}\pi {R_2}^2{h_2} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \) (cm3).
Thể tích hình tạo thành là: \(V = {V_1} + {V_2} = 16\pi + 128\pi = 144\pi \) (cm3).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
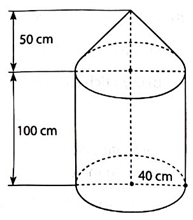
h = 0,6 m = 60 cm; R = \(\frac{4}{2}\) = 2 cm.
Diện tích xung quanh của bóng đèn là: \({S_{xq}} = 2\pi Rh = 2\pi .2.60 = 240\pi \) (cm2).
Thể tích của bóng đèn là: \(V = \pi {R^2}h = \pi {.2^2}.60 = 240\pi \) (cm3).
Lời giải
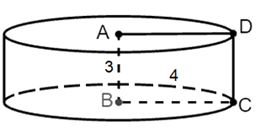
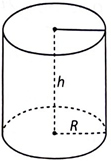
R = 4 cm, h = 3 cm.
Diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .4.3 = 24\pi \) (cm2).
Thể tích của hình trụ là: \(V = \pi {R^2}h = \pi {.4^2}.3 = 48\pi \) (cm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.