Câu hỏi:
19/09/2024 1,831
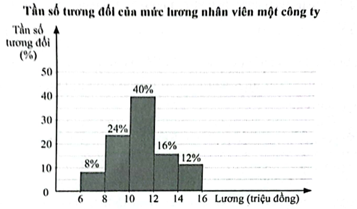
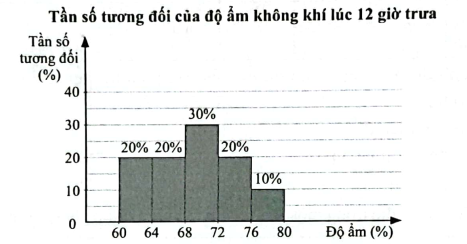
Trong một giải bóng đá, số cổ động viên đến sân cổ vũ mỗi trận đấu được ghi lại ở bảng sau (đơn vị: nghìn người):
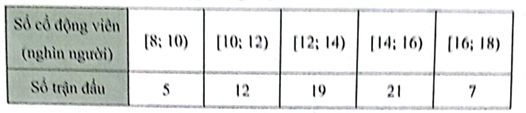
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?
A. 2,48.
B. 4,93.
C. 3,31.
D. 5,11.
Trong một giải bóng đá, số cổ động viên đến sân cổ vũ mỗi trận đấu được ghi lại ở bảng sau (đơn vị: nghìn người):
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị nào dưới đây?
A. 2,48.
B. 4,93.
C. 3,31.
D. 5,11.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
Ta có: \(\frac{n}{4} = \frac{{64}}{4} = 16\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x16 ∈ [10; 12).
Do đó, Q1 = 10 + \(\frac{{16 - 5}}{{12}}\left( {12 - 10} \right)\) = 12.
Ta có: \(\frac{{3n}}{4} = \frac{{3.64}}{4} = 48\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x48 ∈ [14; 16).
Do đó, Q3 = 14 + \(\frac{{48 - \left( {5 + 12 + 19} \right)}}{{21}}\left( {16 - 14} \right)\) = \(\frac{{106}}{7}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là:
∆Q = Q3 – Q1 = \(\frac{{106}}{7}\) − 12 ≈ 3,143.
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần nhất với giá trị 3,31.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
Số trung bình của mẫu số liệu là:
\(\overline x \) = \(\frac{{9.5 + 11.12 + 13.19 + 15.21 + 17.7}}{{64}}\) = 13,40625.
Phương sai của mẫu số liệu trên là:
s2 = \(\frac{{{9^2}.5 + {{11}^2}.12 + {{13}^2}.19 + {{15}^2}.21 + {{17}^2}.7}}{{64}} - 13,{40625^2}\) ≈ 4,897.
Độ lệch chuẩn của mẫu số liệu là:
s ≈ \(\sqrt {4,897} \) ≈ 2,21.
Lời giải
|
a) 2 |
b) 10 |
c) 113 |
d) 71 |
Dựa vào biểu đồ trên, ta có bảng sau:
Tần số của nhóm [6; 8) là 25.8% = 2 (nhân viên).
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: R = 16 – 6 = 10.
Ta có: \(\frac{n}{4} = \frac{{25}}{4} = 6,25\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là x7 ∈ [8; 10).
Do đó, Q1 = 8 + \(\frac{{6,25 - 2}}{6}\left( {10 - 8} \right)\) = \(\frac{{113}}{{12}}\).
Ta có: \(\frac{{3n}}{4} = \frac{{3.25}}{4} = 18,75\).
Tứ phân vị thứ ba của mẫu số liệu gốc là x19 ∈ [12; 14).
Do đó, Q3 = 12 + \(\frac{{18,75 - \left( {2 + 6 + 10} \right)}}{4}\left( {14 - 12} \right)\) = \(\frac{{99}}{8}\).
Khoảng tứ phân vị của mẫu số liệu là:
∆Q = Q3 – Q1 = \(\frac{{99}}{8}\) − \(\frac{{113}}{{12}}\) = \(\frac{{71}}{{24}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)