Người ta quan sát một nhóm người trưởng thành trong 5 năm. Ở thời điểm bắt đầu quan sát, có 30% số người được quan sát thường xuyên hút thuốc. Sau 5 năm, người ta nhận thấy tỉ lệ tử vong trong số những người thường xuyên hút thuốc cao gấp 3 lần tỉ lệ này trong nhóm những người còn lại. Chọn ngẫu nhiên một người trong nhóm và thấy người này tử vong trong 5 năm quan sát, tính xác suất người đó thường xuyên hút thuốc.

Xem lời giải

Câu hỏi trong đề: Giải SBT Toán 12 Chân trời sáng tạo Bài tập cuối chương VI có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Gọi A là biến cố “Một người tử vong trong 5 năm quan sát” và B là biến cố “Một người thường xuyên hút thuốc”.

Do thời điểm bắt đầu quan sát, có 30% số người được quan sát thường xuyên hút thuốc nên P(B) = 0,3 và P(\[\overline B \]) = 1 – 0,3 = 0,7.

Gọi tỉ lệ tử vong trong số những người không thường xuyên hút thuốc là a (0 ≤ a ≤ 1).

Do ở thời điểm sau 5 năm, người ta nhận thấy tỉ lệ tử vong trong số những người thường xuyên hút thuốc cao gấp 3 lần tỉ lệ này trong nhóm những người còn lại nên

P(A | \[\overline B \]) = a và P(A | B) = 3a.

Theo công thức xác suất toàn phần, tỉ lệ một người tử vong trong 5 năm quan sát là:

P(A) = P(B)P(A | B) + P(\[\overline B \])P(A | \[\overline B \]) = 0,3.3a + 0,7a = 1,6a.

Theo công thức Bayes, xác suất một người thường xuyên hút thuốc, biết rằng người đó tử vong trong 5 năm quan sát là:

P(B | A) = \[\frac{{P\left( B \right)P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{0,3.3a}}{{1,6a}}\] = 0,5625.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hộp thứ nhất chứa 5 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 4 viên bi đỏ. Chọn ngẫu nhiên 3 viên bi từ hộp thứ nhất và bỏ vào hộp thứ hai, rồi từ hộp thứ hai chọn ra ngẫu nhiên 2 viên bi.

a) Tính xác suất của biến cố 2 viên bi lấy ra ở hợp thứ hai có cùng màu.

b) biết 2 viên bi lấy ra ở hợp thứ hai có cùng màu, tính xác suất 3 viên bi lấy ra từ hộp thứ nhất cũng có cũng màu.

Xem đáp án

Lời giải

a) Ta có sơ đồ hình cây sau:

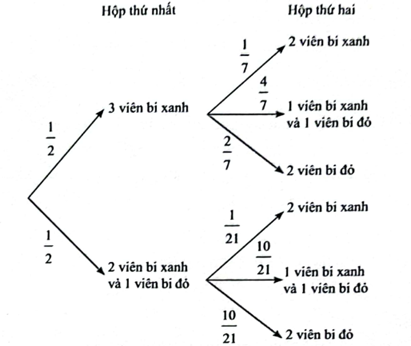
Hộp thứ nhất chứa 5 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 4 viên bi đỏ. Chọn ngẫu nhiên 3 viên bi từ hộp thứ nhất và bỏ vào hộp thứ hai, rồi từ hộp thứ hai chọn ra ngẫu nhiên 2 viên bi. (ảnh 1)

Gọi A là biến cố “2 viên bi ở hộp thứ hai lấy ra có cùng màu” và B là biến cố “3 viên bi lấy ra từ hộp thứ nhất có cùng màu”.

Từ biểu đồ hình cây, ta có xác suất của biến cố 2 viên bi lấy ra ở hộp thứ hai có cùng màu là P(A) = \[\frac{1}{2}\left( {\frac{1}{7} + \frac{2}{7}} \right) + \frac{1}{2}\left( {\frac{1}{{21}} + \frac{{10}}{{21}}} \right) = \frac{{10}}{{21}}\]≈ 0,476.

b) xác suất của biến cố 3 viên bi lấy ra từ hộp thứ nhất có cùng màu là P(B) = \[\frac{1}{2}\].

Xác suất của biến cố 2 viên bi lấy ra ở hộp thứ hai có cùng màu, biết rằng 3 viên bi lấy ra ở hộp thứ nhất có cùng màu là P(A | B) = \[\frac{1}{7} + \frac{2}{7} = \frac{3}{7}\].

Theo công thức Bayes, xác suất 3 viên bi lấy ra ở hộp thứ nhất có cùng màu, biết rằng 2 viên bi lấy ra ở hộp thứ hai có cùng màu là:

P(B | A) \[ = \frac{{P\left( B \right)P\left( {A|B} \right)}}{{P\left( A \right)}} = \frac{{\frac{1}{2}.\frac{3}{7}}}{{\frac{{10}}{{21}}}} = 0,45\].

Câu 2

Cho sơ đồ hình cây dưới đây:

a) Xác suất của biến cố B với điều kiện A không xảy ra là 0,6.

b) Xác suất cả hai biến cố A và B đều không xảy ra là 0,3.

c) Xác suất của biến cố B là 0,9.

d) Xác suất của biến cố A với điều kiện B là \(\frac{1}{{19}}.\)

Xem đáp án

Lời giải

a) Đ

b) S

c) S

d) Đ

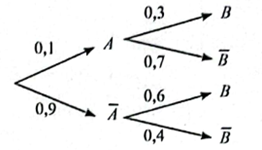
a) Quan sát sơ đồ hình cây, ta thấy xác suất của biến cố B với điều kiện A không xảy ra là 0,6.

b) Quan sát sơ đồ hình cây, ta thấy xác suất cả hai biến cố A và B đều không xảy ra là 0,4.

c) Ta có: P(B) = P(A).P(B | A) + P(\[\overline A \]).P(B | \[\overline A \]) = 0,1.0,3 + 0,9.0,6 = 0,57.

d) Ta có: P(A | B) = \[\frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{0,1.0,3}}{{0,57}} = \frac{1}{{19}}\]

Câu 3