Câu hỏi:
22/09/2024 312
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) thoả mãn hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) liên tục trên \(\mathbb{R}\) và cắt Ox tại đúng 3 điểm phân biệt có hoành độ \({\rm{a}},{\rm{b}},{\rm{c}}\) (hinh bên). Gọi \({{\rm{S}}_1}\) là diện tích của hình phẳng giới hạn bởi đổ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{b}}],{{\rm{S}}_2}\) là diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = {{\rm{f}}^\prime }({\rm{x}})\) và Ox tương ứng với \({\rm{x}} \in [{\rm{b}};{\rm{c}}].\)
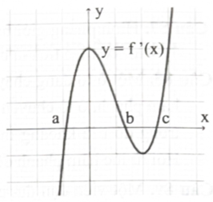
a) \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\quad \forall {\rm{x}} \in [{\rm{a}};{\rm{b}}],{{\rm{f}}^\prime }({\rm{x}}) \le 0\quad \forall {\rm{x}} \in [{\rm{b}};{\rm{c}}].\)
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) thoả mãn hàm \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) liên tục trên \(\mathbb{R}\) và cắt Ox tại đúng 3 điểm phân biệt có hoành độ \({\rm{a}},{\rm{b}},{\rm{c}}\) (hinh bên). Gọi \({{\rm{S}}_1}\) là diện tích của hình phẳng giới hạn bởi đổ thị hàm số \({\rm{y}} = {{\rm{f}}^\prime }({\rm{x}})\) và Ox tương ứng với \({\rm{x}} \in [{\rm{a}};{\rm{b}}],{{\rm{S}}_2}\) là diện tích của hình phẳng giới hạn bởi đồ thị hàm số \(y = {{\rm{f}}^\prime }({\rm{x}})\) và Ox tương ứng với \({\rm{x}} \in [{\rm{b}};{\rm{c}}].\)
a) \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\quad \forall {\rm{x}} \in [{\rm{a}};{\rm{b}}],{{\rm{f}}^\prime }({\rm{x}}) \le 0\quad \forall {\rm{x}} \in [{\rm{b}};{\rm{c}}].\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) \({{\rm{f}}^\prime }({\rm{x}}) \ge 0\forall {\rm{x}} \in [{\rm{a}};{\rm{b}}],{{\rm{f}}^\prime }({\rm{x}}) \le 0\forall {\rm{x}} \in [{\rm{b}};{\rm{c}}].\)
=> Đúng
Câu hỏi cùng đoạn
Câu 2:
b) Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên [a;b] và nghịch biến trên [b; c].
b) Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên [a;b] và nghịch biến trên [b; c].
Lời giải của GV VietJack
b) Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) đồng biến trên [a;b] và nghịch biến trên [b; c].
=> Sai
Câu 3:
c) \({S_1} = f(a) - f(b),{S_2} = f(a) - f(c).\)
c) \({S_1} = f(a) - f(b),{S_2} = f(a) - f(c).\)
Lời giải của GV VietJack
c) \({S_1} = \int_a^b {\left| {{f^\prime }(x)} \right|} dx = \int_a^b {{f^\prime }} (x)dx = f(b) - f(a).\)
\({S_2} = \int_b^c {\left| {{f^\prime }(x)} \right|} dx = \int_b^c - {f^\prime }(x)dx = f(b) - f(c).\)
=> Sai
Câu 4:
d) \(f(\) b) \( > f(c) > f(\) a \().\)
d) \(f(\) b) \( > f(c) > f(\) a \().\)
Lời giải của GV VietJack
d) \({\rm{f}}({\rm{x}})\) nghịch biến trên \([{\rm{b}};{\rm{c}}]\) nên \({\rm{f}}({\rm{b}}) > {\rm{f}}({\rm{c}}).\)
\({S_1} > {S_2}\) nên \(f(b) - f(a) > f(b) - f(c)\), suy ra \(f(c) > f(a).\)
Vậy \(f(b) > f(c) > f(a).\)
=> Đúng
Nhà sách vietjack
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Hoành độ giao điểm của đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và Ox là nghiệm của phương trình \({\rm{f}}({\rm{x}}) = 0.\)
a) Hoành độ giao điểm của đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và Ox là nghiệm của phương trình \({\rm{f}}({\rm{x}}) = 0.\)
Xem đáp án »
22/09/2024
979
Câu 2:
a) Hoành độ giao điểm của đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và Ox là nghiệm của phương trình \({\rm{f}}({\rm{x}}) = 0.\)
a) Hoành độ giao điểm của đồ thị hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) và Ox là nghiệm của phương trình \({\rm{f}}({\rm{x}}) = 0.\)
Xem đáp án »
22/09/2024
715
Câu 3:
a) \(f(x) = \frac{1}{{{x^{\frac{9}{7}}}}},x \in (0; + \infty ).\)
a) \(f(x) = \frac{1}{{{x^{\frac{9}{7}}}}},x \in (0; + \infty ).\)
Xem đáp án »
22/09/2024
615
Câu 4:
a) Quãng đường \({\rm{s}}({\rm{t}})\) chất điểm đó chuyển động trên trục Ox từ thời điểm nào đó đến thời điểm t thoả mãn \({{\rm{s}}^\prime }({\rm{t}}) = {\rm{f}}({\rm{t}}).\)
a) Quãng đường \({\rm{s}}({\rm{t}})\) chất điểm đó chuyển động trên trục Ox từ thời điểm nào đó đến thời điểm t thoả mãn \({{\rm{s}}^\prime }({\rm{t}}) = {\rm{f}}({\rm{t}}).\)
Xem đáp án »
22/09/2024
541
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
50 bài tập Nguyên hàm, tích phân và ứng dụng có lời giải
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận