Cho hàm số \(f(x) = \cot x,x \ne k\pi ,\forall k \in \mathbb{Z}.\)
Cho hàm số \({\rm{f}}({\rm{x}}) = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) với \({\rm{ac}} \ne 0,{\rm{ad}} - {\rm{bc}} > 0.\)
a) \({f^\prime }(x) = \frac{{ad - bc}}{{{{(cx + d)}^2}}}.\)
Cho hàm số \(f(x) = \cot x,x \ne k\pi ,\forall k \in \mathbb{Z}.\)
Cho hàm số \({\rm{f}}({\rm{x}}) = \frac{{{\rm{ax}} + {\rm{b}}}}{{{\rm{cx}} + {\rm{d}}}}\) với \({\rm{ac}} \ne 0,{\rm{ad}} - {\rm{bc}} > 0.\)
a) \({f^\prime }(x) = \frac{{ad - bc}}{{{{(cx + d)}^2}}}.\)
Câu hỏi trong đề: (2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5) !!
Quảng cáo
Trả lời:
Đúng
Câu hỏi cùng đoạn
Câu 2:
b) Hàm số nghịch biến trên từng khoảng xác định \(\left( { - \infty ;\frac{{ - {\rm{d}}}}{{\rm{c}}}} \right),\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}}; + \infty } \right).\)
b) Hàm số nghịch biến trên từng khoảng xác định \(\left( { - \infty ;\frac{{ - {\rm{d}}}}{{\rm{c}}}} \right),\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}}; + \infty } \right).\)
Sai
Câu 3:
c) Đồ thị hàm số có đường tiệm cận đứng là \({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}\) và đường tiệm cận ngang là \(x = - \frac{d}{c}\)
c) Đồ thị hàm số có đường tiệm cận đứng là \({\rm{y}} = \frac{{\rm{a}}}{{\rm{c}}}\) và đường tiệm cận ngang là \(x = - \frac{d}{c}\)
Sai
Câu 4:
d) Đồ thị hàm số có tâm đối xứng là \({\rm{I}}\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}};\frac{{\rm{a}}}{{\rm{c}}}} \right).\)
d) Đồ thị hàm số có tâm đối xứng là \({\rm{I}}\left( {\frac{{ - {\rm{d}}}}{{\rm{c}}};\frac{{\rm{a}}}{{\rm{c}}}} \right).\)
Đúng
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp số: 38,2.
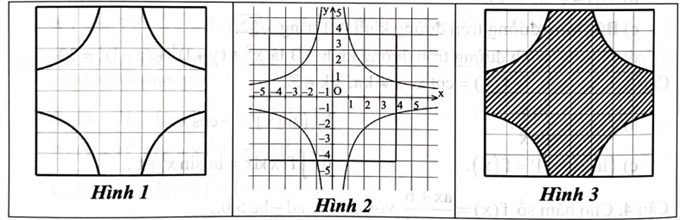
Diện tích hình vuông cạnh 8 dm là \(64{\rm{d}}{{\rm{m}}^2}.\)
Diện tích một góc viên gạch phần không sơn hồng là \(\int_1^4 {\left| {\frac{{ - 4}}{{\rm{x}}} - ( - 4)} \right|} {\rm{dx}}\left( {{\rm{d}}{{\rm{m}}^2}} \right).\)
Diện tích phần sơn màu hồng là: \(64 - 4\int_1^4 {\left| {\frac{{ - 4}}{{\rm{x}}} - ( - 4)} \right|} {\rm{dx}} \approx 38,2\left( {{\rm{d}}{{\rm{m}}^2}} \right).\)
Lời giải
Đáp số: 7,5.
Giả sử hình hộp chữ nhật có chiều rộng của đáy là x, chiều dài của đáy là 3 x, chiều cao là y (đơn vị \({\rm{m}},{\rm{x}} > 0,{\rm{y}} > 0\) ).
Ta có: \(3x \cdot x + 2 \cdot x \cdot y + 2 \cdot 3x \cdot y = 20\), tức là \(3{x^2} + 8xy = 20,y = \frac{{20 - 3{x^2}}}{{8x}}.\)
Thể tích của bể cá là \(V = 3{\rm{x}} \cdot {\rm{x}} \cdot {\rm{y}} = 3{\rm{x}} \cdot {\rm{x}} \cdot \frac{{20 - 3{{\rm{x}}^2}}}{{8{\rm{x}}}} = \frac{3}{8}\left( { - 3{{\rm{x}}^3} + 20{\rm{x}}} \right).\)
\(f(x) = \frac{3}{8}\left( { - 3{x^3} + 20x} \right),0 < x < \sqrt {\frac{{20}}{3}} .\)
\({f^\prime }(x) = \frac{3}{8}\left( { - 9{x^2} + 20} \right),{f^\prime }(x) = 0 \Leftrightarrow x = \frac{{2\sqrt 5 }}{3}.\)
Lập bảng biến thiên của hàm số trên \(\left( {0;\sqrt {\frac{{20}}{3}} } \right)\), thể tích có giá trị lớn nhất là \(\frac{3}{8}\left[ { - 3 \cdot {{\left( {\frac{{2\sqrt 5 }}{3}} \right)}^3} + 20 \cdot \left( {\frac{{2\sqrt 5 }}{3}} \right)} \right] = \frac{{10\sqrt 5 }}{3} \approx 7,5\left( {\;{{\rm{m}}^3}} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \({30^o }.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình lập phương \(ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }.\) Số đo góc nhị diện \(\left[ {{C^\prime },{\rm{AB}},{\rm{C}}} \right]\) bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/09/blobid2-1727161807.png)