Quan sát bảng biến thiên dưới đây và cho biết bảng biến thiên đó là của hàm số nào?
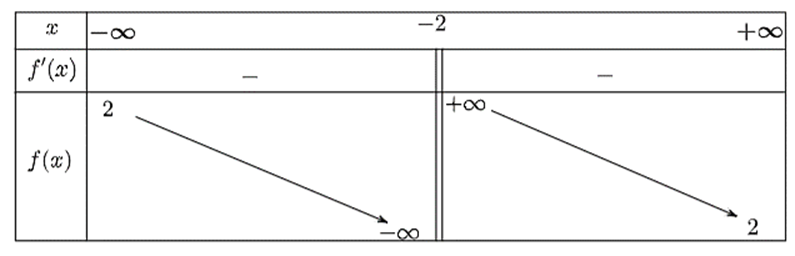
Quan sát bảng biến thiên dưới đây và cho biết bảng biến thiên đó là của hàm số nào?

D. \(y = \frac{{2x + 5}}{{x - 2}}\).
Quảng cáo
Trả lời:
Đáp án đúng là: A
Từ bảng biến thiên, ta thấy đồ thị hàm số có tiệm cận đứng là \(x = - 2\) và tiệm cận ngang là \(y = 2\) nên ta loại phương án C và D.
Mặt khác, hàm số đã cho nghịch biến trên các khoảng xác định của nó.
Xét hàm số \(y = \frac{{2x - 3}}{{x + 2}}\), ta có \(y' = \frac{7}{{{{\left( {x + 2} \right)}^2}}} > 0\) nên hàm số đồng biến trên các khoảng xác định của nó, do đó ta loại phương án B.
Xét hàm số \(y = \frac{{2x + 5}}{{x + 2}}\), ta có \(y' = \frac{{ - 1}}{{{{\left( {x + 2} \right)}^2}}} < 0\) nên hàm số nghịch biến trên các khoảng xác định của nó, do đó ta chọn phương án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
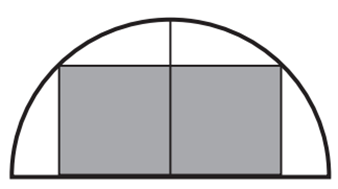
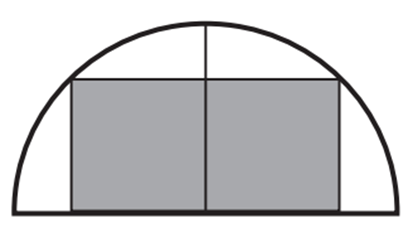
Gọi \(x\,\,\left( {{\rm{cm}}} \right)\) là độ dài một cạnh của tấm giấy hình chữ nhật được cắt ra (cạnh thuộc đường kính) và \(y\,\,\left( {{\rm{cm}}} \right)\) là độ dài cạnh còn lại \((0 < x < 16,\,\,0 < y < 8)\). Ta có:
\({\left( {\frac{x}{2}} \right)^2} + {y^2} = {8^2} \Leftrightarrow {y^2} = \frac{1}{4}\left( {256 - {x^2}} \right) \Leftrightarrow y = \frac{1}{2}\sqrt {256 - {x^2}} \).
Diện tích của tấm giấy hình chữ nhật đó là:
\(S = xy = x \cdot \frac{1}{2}\sqrt {256 - {x^2}} = \frac{1}{2}\sqrt {{x^2}\left( {256 - {x^2}} \right)} \) (cm2).
Đặt \(f\left( x \right) = {x^2}\left( {256 - {x^2}} \right)\) với \(0 < x < 16\), có \(f'\left( x \right) = 512x - 4{x^3}\) nên \(f'\left( x \right) = 0\) khi \(x = 8\sqrt 2 \).
Vậy giá trị lớn nhất của \(S\) bằng \(\frac{1}{2}\sqrt {f\left( {8\sqrt 2 } \right)} = 64\,\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Đáp số: \(64\).
Lời giải
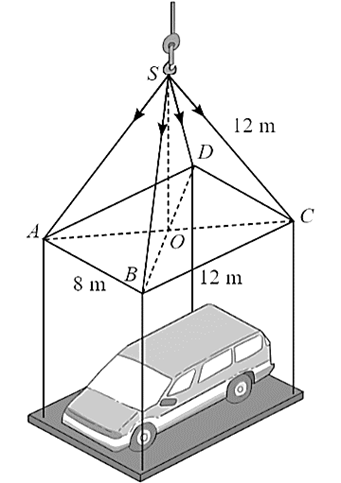
Gọi độ dài cạnh đáy của thùng chứa gạo là \(x\) (m, \(x > 0\)) và chiều cao của thùng chứa gạo là \(h\) (m, \(h > 0\)).
Thể tích của thùng là \(V = {x^2} \cdot h = 2\), suy ra \(h = \frac{2}{{{x^2}}}\) (m).
Khi đó, diện tích tôn cần sử dụng là: \[S = {x^2} + 4xh = {x^2} + 4x \cdot \frac{2}{{{x^2}}} = {x^2} + \frac{8}{x}\] (m2).
Chi phí để mua nguyên liệu là: \(T = 100{x^2} + 50 \cdot \frac{8}{x} = 100{x^2} + \frac{{400}}{x}\) (nghìn đồng).
Xét hàm số \(T\left( x \right) = 100{x^2} + \frac{{400}}{x}\) với \(x \in \left( {0; + \infty } \right)\).
Ta có: \(T'\left( x \right) = 200x - \frac{{400}}{{{x^2}}} = \frac{{200{x^3} - 400}}{{{x^2}}}\); \(T'\left( x \right) = 0\) khi \(x = \sqrt[3]{2}\).
Bảng biến thiên của hàm số \(T\left( x \right)\) trên khoảng \(\left( {0; + \infty } \right)\) như sau:
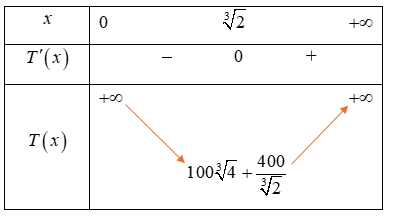
Từ bảng biến thiên ta thấy, \(T\left( x \right)\) đạt giá trị nhỏ nhất trên \(\left( {0; + \infty } \right)\) khi \(x = \sqrt[3]{2}\).
Vậy ông Hùng cần đóng thùng chứa gạo với cạnh đáy bằng \(\sqrt[3]{2} \approx 1,3\) m để chi phí mua nguyên liệu là nhỏ nhất.
Đáp số: \(1,3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
D. \(\left( {4;\, + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.